题目内容
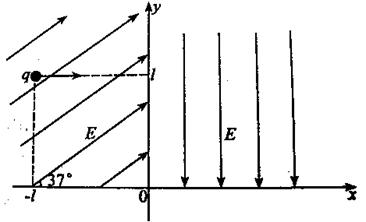
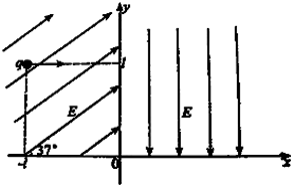 如图xOy平面坐标系,x轴方向为水平方向,y轴方向为竖直方向,在第一象限内有竖直向下的匀强电场E,在第二象限内场强为E的匀强电场与x轴正方向成37°(sin37°=0.6,cos37°=0.8),在(-l,l)处一带电荷量为q的带电小球由静止开始沿x轴正方向直线运动,然后进入第一象限.求:
如图xOy平面坐标系,x轴方向为水平方向,y轴方向为竖直方向,在第一象限内有竖直向下的匀强电场E,在第二象限内场强为E的匀强电场与x轴正方向成37°(sin37°=0.6,cos37°=0.8),在(-l,l)处一带电荷量为q的带电小球由静止开始沿x轴正方向直线运动,然后进入第一象限.求:(1)带电小球第一次经过x轴时的位置坐标
(2)带电小球第一次经过x轴是的动能.
分析:(1)小球在第二象限内做直线运动,知合力的方向水平向右,根据竖直方向上平衡得出重力与电场力的关系,对第二象限内的运动过程运用动能定理得出进入第一象限的初速度,结合类平抛运动的规律,通过牛顿第二定律和运动学公式求出带电小球第一次经过x轴时的位置坐标.
(2)对全过程运用动能定理,结合重力和电场力的关系求出带电小球第一次经过x轴时的动能.
(2)对全过程运用动能定理,结合重力和电场力的关系求出带电小球第一次经过x轴时的动能.
解答:解:(1)设小球所受的重力为G,小球在第二象限内做直线运动,知小球合力水平向右,竖直方向上合力为零.
有:G=qEsin37°.
设进入第一象限的初速度为v0
根据动能定理得,qElcos37°=
mv02.
小球在第一象限内,竖直方向上有:l=
at2,a=
水平方向上有:x=v0t
联立各式解得x=
l.
(2)对全过程运用动能定理得,qElcos37°+(qE+G)l=Ek
解得Ek=
qEl.
答:(1)带电小球第一次经过x轴时的位置坐标为x=
l.(2)带电小球第一次经过x轴是的动能为Ek=
qEl.
有:G=qEsin37°.
设进入第一象限的初速度为v0
根据动能定理得,qElcos37°=
| 1 |
| 2 |
小球在第一象限内,竖直方向上有:l=
| 1 |
| 2 |
| qE+G |
| m |
水平方向上有:x=v0t
联立各式解得x=
| 2 |
(2)对全过程运用动能定理得,qElcos37°+(qE+G)l=Ek
解得Ek=
| 12 |
| 5 |
答:(1)带电小球第一次经过x轴时的位置坐标为x=
| 2 |
| 12 |
| 5 |
点评:解决本题的关键知道小球在第二象限内做匀加速直线运动,合力水平向右,在第一象限内做类平抛运动,结合动能定理和牛顿第二定律进行求解.

练习册系列答案
相关题目
 处一带电荷量为q的带电小球由静止开始沿x轴正方向直线运动,然后进入第一象限。求:
处一带电荷量为q的带电小球由静止开始沿x轴正方向直线运动,然后进入第一象限。求:
 处一带电荷量为q的带电小球由静止开始沿x轴正方向直线运动,然后进入第一象限。求:
处一带电荷量为q的带电小球由静止开始沿x轴正方向直线运动,然后进入第一象限。求: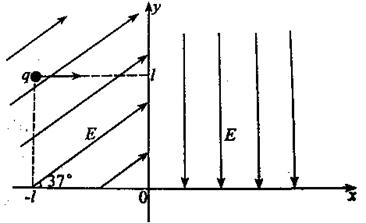
 处一带电荷量为q的带电小球由静止开始沿x轴正方向直线运动,然后进入第一象限。求:
处一带电荷量为q的带电小球由静止开始沿x轴正方向直线运动,然后进入第一象限。求: