题目内容
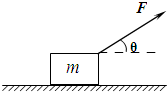（2007?深圳一模）如图所示，质量为m的金属块放在水平桌面上，在与水平方向成θ角斜向上、大小为F的拉力作用下，以速度v向右做匀速直线运动．重力加速度为g．（1）求金属块与桌面间的动摩擦因数；
（2）如果从某时刻起撤去拉力，则撤去拉力后金属块在桌面上还能滑行多远？
分析：（1）分析金属块的受力情况，根据平衡条件和滑动摩擦力公式求解动摩擦因数；
（2）撤去拉力后金属块水平方向只受滑动摩擦力，根据牛顿第二定律求出加速度，再由位移速度公式求解金属块在桌面上滑行的最大距离．
（2）撤去拉力后金属块水平方向只受滑动摩擦力，根据牛顿第二定律求出加速度，再由位移速度公式求解金属块在桌面上滑行的最大距离．
解答：解：（1）对金属块受力分析，受拉力、重力、支持力、摩擦力，如图所示：
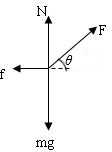
因为金属块匀速运动，受力平衡则有
Fcosθ-μ（mg-Fsinθ）=0
得μ=
（2）撤去拉力后金属块的加速度大小为：a=-
=-μg=-
金属块在桌面上滑行的最大距离：s=
=
答：（1）金属块与桌面间的动摩擦因数为
；
（2）撤去拉力后金属块在桌面上滑行的最大距离为
．
因为金属块匀速运动，受力平衡则有
Fcosθ-μ（mg-Fsinθ）=0
得μ=
| Fcosθ |
| mg-Fsinθ |
（2）撤去拉力后金属块的加速度大小为：a=-
| f |
| m |
| Fgcosθ |
| mg-Fsinθ |
金属块在桌面上滑行的最大距离：s=
| -v2 |
| 2a |
| v2(mg-Fsinθ) |
| 2Fgcosθ |
答：（1）金属块与桌面间的动摩擦因数为
| Fcosθ |
| mg-Fsinθ |
（2）撤去拉力后金属块在桌面上滑行的最大距离为
| v2(mg-Fsinθ) |
| 2Fgcosθ |
点评：本题是物体的平衡问题，关键是分析物体的受力情况，作出力图．要注意撤去F后动摩擦因数不变．
练习册系列答案
新课标阶梯阅读训练系列答案
口算心算速算应用题系列答案
同步拓展阅读系列答案
相关题目
（2007?深圳一模）如图所示，有两个光滑固定斜面AB和BC，A和C两点在同一水平面上，斜面BC比斜面AB长，一个滑块自A点以速度vA上滑，到达B点时速度减小为零，紧接着沿BC滑下，设滑块从A点到C点的总时间是tc，那么下列四个图中，正确表示滑块速度大小v随时间t变化规律的是（ ）
（2007?深圳一模）已知可见光的光子能量范围约为1.62eV～3.11eV．一群氢原子处于n=4的激发态，则关于这些氢原子可能产生的光谱线，下列说法中正确的是（ ）
（2007?深圳一模）如图所示，一列振幅为5cm，频率为10Hz，水平向右传播的横波，波速为20m/s，沿波传播的方向上依次有a、b两个质点，相距5.5m．则下列说法中正确的是（ ）
（2007?深圳一模）（1）如图甲所示，要研究光敏电阻的阻值与光照强弱的关系．
（2007?深圳一模）如图所示，用导电的金属丝吊着的一块金属板，与装有电子枪的电源相连，从电子枪发出的电子的初速度为零，用电压U将电子加速后，电子与金属板垂直碰撞．假设所有电子碰撞金属板之后，全部被金属板吸收，已知电子的电荷量和质量分别为-e （e＞0）和m．试求：