题目内容
已知地球的质量为M,引力常量为G,设飞船绕地球做匀速圆周运动的轨道半径为r,则飞船在圆轨道上运行的速率为()
A. 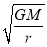 B.
B. 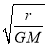 C.
C. 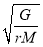 D.
D. 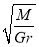
练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目
题目内容
已知地球的质量为M,引力常量为G,设飞船绕地球做匀速圆周运动的轨道半径为r,则飞船在圆轨道上运行的速率为()
A. 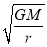 B.
B. 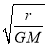 C.
C. 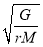 D.
D. 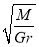
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案