题目内容
20.玻璃生产线的最后有一台切割机,能将一定宽度但很长的原始玻璃板按需要的长度切成矩形.假设送入切割机的原始玻璃板的宽度是L=2m,它沿切割机的轨道(与玻璃板的两侧边平行)以v1=0.15m/s的速度水平向右匀速移动;已知割刀相对玻璃的切割速度v2=0.2m/s,为了确保割下的玻璃板是矩形,则相对地面参考系( )| A. | 割刀运动的轨迹是一段直线 | |
| B. | 割刀完成一次切割的时间为10s | |
| C. | 割刀运动的实际速度为0.05$\sqrt{7}$m/s | |
| D. | 割刀完成一次切割的时间内,玻璃板的位移是1.5m |
分析 割刀实际参与两个分运动,即沿玻璃的运动和垂直玻璃方向的运动.根据运动的合成确定运动的轨迹以及合速度.根据分运动与合运动具有等时性,求出完成一次切割所需的时间,以及一次切割时间里玻璃板的位移.
解答 解:A、为了使割下的玻璃板都成规定尺寸的矩形,割刀相对玻璃的运动速度应垂直玻璃.割刀实际参与两个分运动,即沿玻璃的运动和垂直玻璃方向的运动.两个分运动都是匀速直线运动,则合运动为匀速直线运动.故A正确.
B、对于垂直玻璃方向的运动,运动时间t=$\frac{2}{0.2}$=10s.故B正确.
C、割刀运动的实际速度v=$\sqrt{{v}_{1}^{2}+{v}_{2}^{2}}$=$\sqrt{0.1{5}^{2}+0.{2}^{2}}$=0.25m/s.故C错误.
D、10s内玻璃在水平方向的运动位移x=v1t=1.5m.故D正确.
故选:ABD.
点评 解决本题的关键知道割刀实际参与两个分运动,即沿玻璃的运动和垂直玻璃方向的运动.知道合运动与分运动具有等时性,以及会用平行四边形定则求合速度.

练习册系列答案
相关题目
9.如图所示的四图中,A、B两图是质量均为m的小球以相同的水平初速度向右抛出,A图只受重力作用,B图除受重力外还受水平向右的恒定风力作用;C、D两图中有相同的无限宽的电场,场强方向竖直向下,D图中还有垂直于纸面向里无限宽的匀强磁场且和电场正交,在两图中均以相同的初速度向右水平抛出质量为m的正电荷,两图中不计重力作用,则下列有关说法正确的是( )
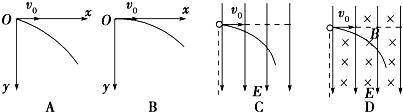

| A. | A、B、C三图中的研究对象均做匀变速曲线运动 | |
| B. | 从开始抛出经过相同时间C、D两图竖直方向速度变化相同,A、B两图竖直方向速度变化相同 | |
| C. | 从开始抛出到沿电场线运动相等距离的过程内C、D两图中的研究对象动能变化相同 | |
| D. | 相同时间内A、B两图中的研究对象在竖直方向的动能变化相同 |
 =10m/s的速度在平直道路上行驶,发现前方s=15m处由减速带,立刻刹车匀减速前进,到达减速带时速度v=5.0m/s,已知客车和人的总质量m=
=10m/s的速度在平直道路上行驶,发现前方s=15m处由减速带,立刻刹车匀减速前进,到达减速带时速度v=5.0m/s,已知客车和人的总质量m=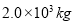 ,求:
,求: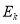 ;
; 。
。 一水平浅色足够长传送带,t=0时刻由静止开始以恒定的加速度a0向右运动,当其速度达到V0后,便以此速度做匀速运动,t=0时刻,一质量为m的煤块(可视为质点)在大小为V0的初速度水平向左抛到传送带上中间某处,经过一段时间,煤块在传送带上留下一段黑色的痕迹后,煤块相对传送带不再滑动,已知煤块与传送带之间动摩擦因数为μ,求:
一水平浅色足够长传送带,t=0时刻由静止开始以恒定的加速度a0向右运动,当其速度达到V0后,便以此速度做匀速运动,t=0时刻,一质量为m的煤块(可视为质点)在大小为V0的初速度水平向左抛到传送带上中间某处,经过一段时间,煤块在传送带上留下一段黑色的痕迹后,煤块相对传送带不再滑动,已知煤块与传送带之间动摩擦因数为μ,求: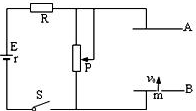 如图所示的电路中,两平行金属板A、B水平放置,两板间的距离d=50cm,电源电动势E=36V,内阻r=1Ω,电阻R=9Ω,闭合开关S,待电路稳定后,将一带正电的微粒从B板小孔以初速度v0=4m/s竖直向上射入两板间,小球恰能到达A板,已知微粒带电质量q=1×10-10C,质量为m=2×10-10kg,不考虑空气阻力和微粒受到的重力,求:
如图所示的电路中,两平行金属板A、B水平放置,两板间的距离d=50cm,电源电动势E=36V,内阻r=1Ω,电阻R=9Ω,闭合开关S,待电路稳定后,将一带正电的微粒从B板小孔以初速度v0=4m/s竖直向上射入两板间,小球恰能到达A板,已知微粒带电质量q=1×10-10C,质量为m=2×10-10kg,不考虑空气阻力和微粒受到的重力,求: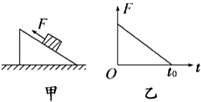 如图甲所示,一物块放在粗糙斜面上,在平行斜面向上的外力F作用下斜面和物块始终处于静止状态,当F按图乙所示规律变化时,物块与斜面间的摩擦力大小变化规律可能是如图答案中的( )
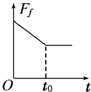
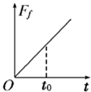
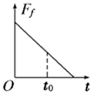
如图甲所示,一物块放在粗糙斜面上,在平行斜面向上的外力F作用下斜面和物块始终处于静止状态,当F按图乙所示规律变化时,物块与斜面间的摩擦力大小变化规律可能是如图答案中的( )
 质量为M=36kg的小孩坐在m=10kg的雪橇上,大人用与水平方向成θ=37°上的F=100N的拉力拉雪橇,他们一起沿水平地面向右做匀速直线运动.(g=10m/s2,sin37°=0.6,cos37°=0.8)求:
质量为M=36kg的小孩坐在m=10kg的雪橇上,大人用与水平方向成θ=37°上的F=100N的拉力拉雪橇,他们一起沿水平地面向右做匀速直线运动.(g=10m/s2,sin37°=0.6,cos37°=0.8)求: 如图所示,质量为M=1.0kg足够长的长木板B静止在光滑水平地面上,在其右端放一质量为m=4.0kg的小铁块A(可视为质点).初始时刻,长木板B的左端距离左侧的墙面为s=1m.现在A上作用一拉力F=10N直至B与墙面第一次相撞,此时立即撤去拉力,设B与墙面相撞后将以原速度弹回而没有机械能损失,A在运动过程中始终没有脱离长木板.已知A、B之间的动摩擦因数μ=0.2,且最大静摩擦力等于滑动摩擦力,重力加速度g=10m/s2.求:
如图所示,质量为M=1.0kg足够长的长木板B静止在光滑水平地面上,在其右端放一质量为m=4.0kg的小铁块A(可视为质点).初始时刻,长木板B的左端距离左侧的墙面为s=1m.现在A上作用一拉力F=10N直至B与墙面第一次相撞,此时立即撤去拉力,设B与墙面相撞后将以原速度弹回而没有机械能损失,A在运动过程中始终没有脱离长木板.已知A、B之间的动摩擦因数μ=0.2,且最大静摩擦力等于滑动摩擦力,重力加速度g=10m/s2.求: