题目内容
(1)如图1所示,螺旋测微器的读数为

(2)学过单摆的周期公式以后,有的同学对钟摆产生了兴趣,他们先研究用厚度和质量分布均匀的方木块(如一把米尺)做成的摆(这种摆被称为复摆),如图2所示.让其在竖直平面内做小角度摆动,C点为重心,板长为L,周期用T表示.
甲同学猜想:复摆的周期应该与板的质量有关.
乙同学猜想:复摆的摆长应该是悬点到重心的距离
.
丙同学猜想:复摆的摆长应该大于
.
为了研究以上猜想是否正确,他们进行了下面的实验探索:T0=2π
,
①把两个相同的木板完全重叠在一起,用透明胶(质量不计)粘好,测量其摆动周期,发现与单个木板摆动时的周期相同,重做多次仍有这样的特点.则证明了甲同学的猜想是
②用T0表示板长为L的复摆看成摆长为L/2单摆的周期计算值用T表示板长为L复摆的实际周期测量值.计算与测量的数据如下表:
由上表可知,复摆的等效摆长
(选填“大于”、“小于”或“等于”).
③为了进一步定量研究,同学们用描点作图法对数据进行处理,所选坐标如图3.请在坐标上作出T-T0图,并根据图象中反映出的规律求出
=
).
0.900
0.900
mm,游标卡尺的读数为33.10
33.10
mm.
(2)学过单摆的周期公式以后,有的同学对钟摆产生了兴趣,他们先研究用厚度和质量分布均匀的方木块(如一把米尺)做成的摆(这种摆被称为复摆),如图2所示.让其在竖直平面内做小角度摆动,C点为重心,板长为L,周期用T表示.
甲同学猜想:复摆的周期应该与板的质量有关.
乙同学猜想:复摆的摆长应该是悬点到重心的距离
| L |
| 2 |
丙同学猜想:复摆的摆长应该大于
| L |
| 2 |
为了研究以上猜想是否正确,他们进行了下面的实验探索:T0=2π
|
①把两个相同的木板完全重叠在一起,用透明胶(质量不计)粘好,测量其摆动周期,发现与单个木板摆动时的周期相同,重做多次仍有这样的特点.则证明了甲同学的猜想是
错误
错误
的(选填“正确”或“错误”).②用T0表示板长为L的复摆看成摆长为L/2单摆的周期计算值用T表示板长为L复摆的实际周期测量值.计算与测量的数据如下表:
| 板长L/cm | 25 | 50 | 80 | 100 | 120 | 150 |
| 周期计算值T0/s | 0.70 | 1.00 | 1.27 | 1.41 | 1.55 | 1.73 |
| 周期测量值T/s | 0.81 | 1.16 | 1.47 | 1.64 | 1.80 | 2.01 |
大于
大于
| L |
| 2 |
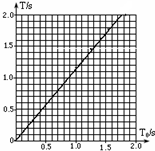
③为了进一步定量研究,同学们用描点作图法对数据进行处理,所选坐标如图3.请在坐标上作出T-T0图,并根据图象中反映出的规律求出
| ||
|
1.16
1.16
(结果保留三位有效数字,其中L等是板长为L时的等效摆长,T=2π
|
分析:(1)游标卡尺的读数等于主尺读数加上游标读数,不需估读;螺旋测微器的读数等于固定刻度读数加上可动刻度读数,需估读.
(2)①根据复摆的周期与质量有无关系,判断甲同学的猜想是否正确.
②根据表格的数据由单摆的周期公式分析复摆的等效摆长与
的关系.
③用描点作图法作出T-To图线.由图线的斜率求出
.
(2)①根据复摆的周期与质量有无关系,判断甲同学的猜想是否正确.
②根据表格的数据由单摆的周期公式分析复摆的等效摆长与
| L |
| 2 |
③用描点作图法作出T-To图线.由图线的斜率求出
| ||||
|
解答:解:(1)螺旋测微器的读数为0.5mm+0.01×40.0=0.900mm,游标卡尺的读数为33mm+0.05×2mm=33.10mm.
(2)①把两个相同的木板完全重叠在一起,用透明胶(质量不计)粘好,测量其摆动周期,发现与单个木板摆动时的周期相同,重做多次仍有这样的特点.知复摆的周期与质量无关.所以甲同学的猜想是错误的.
②因为周期的测量值大于周期的计算值,根据公式知,复摆的等效摆长大于
.
③用描点作图法作出T-To图线如图所示,由数学知识求得:图线的斜率k=
=1.16,则由T=2π
,T0=2π
得,
=1.16.
 故答案为:(1)0.900 33.10
故答案为:(1)0.900 33.10
(2)①错误
②大于
③作图,如图所示,1.16
(2)①把两个相同的木板完全重叠在一起,用透明胶(质量不计)粘好,测量其摆动周期,发现与单个木板摆动时的周期相同,重做多次仍有这样的特点.知复摆的周期与质量无关.所以甲同学的猜想是错误的.
②因为周期的测量值大于周期的计算值,根据公式知,复摆的等效摆长大于
| L |
| 2 |
③用描点作图法作出T-To图线如图所示,由数学知识求得:图线的斜率k=
| T |
| T0 |
|
|
| ||||
|
 故答案为:(1)0.900 33.10
故答案为:(1)0.900 33.10 (2)①错误
②大于
③作图,如图所示,1.16
点评:本题题干较长,首先考查快速获取信息的能力;其次考查知识的迁移能力,用单摆的原理来理解、分析复摆的原理.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目




