题目内容
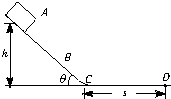
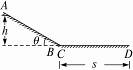
图中ABCD是一条长轨道,其中AB段是倾角为θ的斜面,CD是水平的,BC是与AB和CD都相切的一小段圆弧,其长度可以略去不计,一质量为m的小滑块在A点从静止状态释放,沿轨道滑下,最后停在D点,A点和D点的位置如图所示.现用一沿轨道方向的力推滑块,使它缓慢地由D点推回到A点时停下,设滑块与轨道间的动摩擦因数为μ,则推力做的功等于
- A.μmg(s+h/sinθ)
- B.2μmg(s+hcotθ)
- C.mgh
- D.2mgh
BD
分析题意得,小滑块从A点运动到达D点,应用动能定理得:mgh-Wf=0,得:mgh=Wf,所以第二次若将它现推回到A点,则有动能定理:WF-mgh-Wf=0,所以WF=2mgh,则选项D正确,选项C错.变形公式mgh-Wf=0得:mgh-μmgcosθ=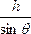 -μmgs=0,所以得mgh=μmg(s+hcotθ),所以选项B也正确.综上所述,本题的正确选项应该为B、D
-μmgs=0,所以得mgh=μmg(s+hcotθ),所以选项B也正确.综上所述,本题的正确选项应该为B、D
分析题意得,小滑块从A点运动到达D点,应用动能定理得:mgh-Wf=0,得:mgh=Wf,所以第二次若将它现推回到A点,则有动能定理:WF-mgh-Wf=0,所以WF=2mgh,则选项D正确,选项C错.变形公式mgh-Wf=0得:mgh-μmgcosθ=
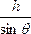 -μmgs=0,所以得mgh=μmg(s+hcotθ),所以选项B也正确.综上所述,本题的正确选项应该为B、D
-μmgs=0,所以得mgh=μmg(s+hcotθ),所以选项B也正确.综上所述,本题的正确选项应该为B、D 
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 图中ABCD是一条长轨道,其中AB段是倾角为θ的斜面,CD段是水平的,BC是与AB和CD都相切的一小段圆弧,其长度可以略去不计.一质量为m的小滑块在A点从静止状态释放,沿轨道滑下,最后停在D点,A点和D点的位置如图所示,现用一沿轨道方向的力推滑块,使它缓缓地由D点推回到A点,设滑块与轨道间的动摩擦系数为μ,则推力对滑块做的功等于( )
图中ABCD是一条长轨道,其中AB段是倾角为θ的斜面,CD段是水平的,BC是与AB和CD都相切的一小段圆弧,其长度可以略去不计.一质量为m的小滑块在A点从静止状态释放,沿轨道滑下,最后停在D点,A点和D点的位置如图所示,现用一沿轨道方向的力推滑块,使它缓缓地由D点推回到A点,设滑块与轨道间的动摩擦系数为μ,则推力对滑块做的功等于( )
 ) D.μmgs+μmgshcosθ
) D.μmgs+μmgshcosθ

 B.
B.
 D.
D.