题目内容
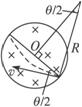
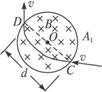
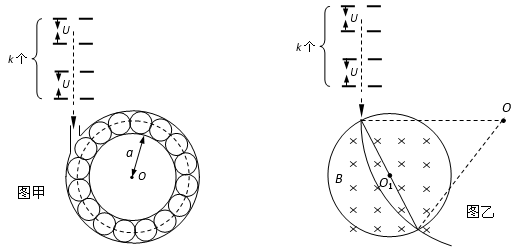
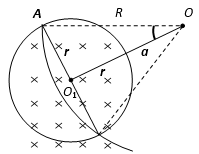
如图甲所示为一种研究高能粒子相互作用的部分简化装置,粒子先由k个加速电场从静止开始加速后,被导入装置送入位于水平面内的圆环型真空管道。每个加速电场电压均为U,在管道内有n个控制粒子转弯的圆形磁场,连续均匀分布在整个圆周上,每个圆形磁场的磁感应强度大小均为B。粒子在环形管道中沿管道中心线做半径为R的匀速圆周运动,经过每个圆形磁场时,入射点和出射点都在同一条直径的两端(如图乙所示)。粒子重力不计,且不考虑粒子的相对论效应,(k、U、R、B、n为已知量)求:
(1)粒子进入圆环型真空管道时的速度大小v;
(2)粒子经过每个圆形磁场区域的时间t;
(3)环形管道的内环半径a.
(1)粒子进入圆环型真空管道时的速度大小v;
(2)粒子经过每个圆形磁场区域的时间t;
(3)环形管道的内环半径a.
解:(1)设粒子质量为m、电荷量为q,由动能定理得:
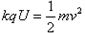 ①
①
又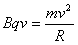 ②
②
得: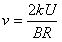 ③
③
(2)由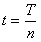 ④
④
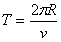 ⑤
⑤
得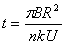 ⑥
⑥
(3)设圆形磁场的区域半径r,在Rt△AO1O中,有:
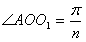 ⑦
⑦
sinπ/n=r/R ⑧
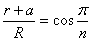 ⑨
⑨
得:a=R(cosπ/n-sinπ/n) ⑩
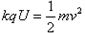 ①
①又
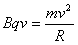 ②
②得:
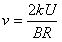 ③
③(2)由
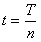 ④
④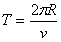 ⑤
⑤得
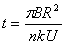 ⑥
⑥(3)设圆形磁场的区域半径r,在Rt△AO1O中,有:
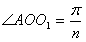 ⑦
⑦sinπ/n=r/R ⑧
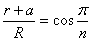 ⑨
⑨得:a=R(cosπ/n-sinπ/n) ⑩


练习册系列答案
相关题目

 (2007?深圳一模)(1)如图甲所示,要研究光敏电阻的阻值与光照强弱的关系.
(2007?深圳一模)(1)如图甲所示,要研究光敏电阻的阻值与光照强弱的关系.