题目内容
14.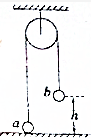 如图所示,不可伸长的柔软细绳跨过光滑定滑轮,细线两端分别系一小球a和b,a球质量为m,静置于地面上,b球质量为M,用手托住,离地面高度为h,此时细绳刚好张紧,从静止开始释放b球后,a球可能达到的最大高度为H(低于滑轮的高度),下列说法中正确的是( )
如图所示,不可伸长的柔软细绳跨过光滑定滑轮,细线两端分别系一小球a和b,a球质量为m,静置于地面上,b球质量为M,用手托住,离地面高度为h,此时细绳刚好张紧,从静止开始释放b球后,a球可能达到的最大高度为H(低于滑轮的高度),下列说法中正确的是( )| A. | 经过时间t=$\sqrt{\frac{(M+m)h}{(M-m)g}}$,两球到达同一高度 | |
| B. | 两球质量之比$\frac{M}{m}$越大,H越大 | |
| C. | 两球质量之比$\frac{M}{m}$满足一定条件,H可以等于2h | |
| D. | 无论a、b两球质量之比$\frac{M}{m}$多大,H都不可能等于2h |
分析 b落地前,根据牛顿第二定律求出加速度,再由位移时间公式求出两球高度相同时所用时间.根据速度位移关系式,可以求得a球上升h时的速度的大小,之后,b球落地,a球的机械能守恒,从而可以求得a球上升的高度的大小,得到H的表达式,再分析即可.
解答 解:A、b落地前,设a、b的加速度大小为a.根据牛顿第二定律得:a=$\frac{Mg-mg}{M+m}$
当a上升$\frac{1}{2}$h时两球到达同一高度,由$\frac{1}{2}$h=$\frac{1}{2}a{t}^{2}$,得 t=$\sqrt{\frac{(M+m)h}{(M-m)g}}$,故A正确.
BCD、设a球到达高度h时两球的速度v,则 v=$\sqrt{2ah}$
b落地后,a球开始做为v做竖直上抛运动,根据机械能守恒:mgh+$\frac{1}{2}$mv2=mgH
解得a球能达到的最大高度 H=$\frac{2M}{M+m}$h=$\frac{2}{1+\frac{m}{M}}$h,则知,$\frac{M}{m}$越大,H越大,H不可能等于2h.故BD正确,C错误.
故选:ABD
点评 本题是连接体问题,要抓住两球的加速度大小相等,运用整体法求解加速度大小,也可以根据系统的机械能守恒求解高度相同时的速度.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
4.如图为一根张紧的绳子上系着五个单摆,让A摆先摆动起来,各摆的摆动情况正确的是( )
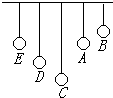

| A. | C摆的振幅最大 | B. | E摆的振幅最大 | ||
| C. | B摆振动周期最小 | D. | 各摆的振动周期相等 |
5.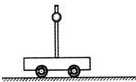 如图所示,水平地面上的小车固定有一竖直的杆,杆上套有一小球,杆表面各处粗糙程度相同.当小车在地面上作直线运动时,小球相对杆匀速下滑,下列对该过程的分析,其中正确的是( )
如图所示,水平地面上的小车固定有一竖直的杆,杆上套有一小球,杆表面各处粗糙程度相同.当小车在地面上作直线运动时,小球相对杆匀速下滑,下列对该过程的分析,其中正确的是( )
 如图所示,水平地面上的小车固定有一竖直的杆,杆上套有一小球,杆表面各处粗糙程度相同.当小车在地面上作直线运动时,小球相对杆匀速下滑,下列对该过程的分析,其中正确的是( )
如图所示,水平地面上的小车固定有一竖直的杆,杆上套有一小球,杆表面各处粗糙程度相同.当小车在地面上作直线运动时,小球相对杆匀速下滑,下列对该过程的分析,其中正确的是( )| A. | 小球不可能作匀速直线运动 | |
| B. | 小球可能作匀变速直线运动 | |
| C. | 小球的位移一定大于小车的位移 | |
| D. | 如果小车的速度均匀增大,小球的速度也均匀增大 |
2. 如图所示,两个小球从水平地面上方同一点O分别以初速度v1、v2水平抛出,落在地面上的位置分别是A和B,O′是O在地面上的竖直投影,且O′A:AB=2:3.若不计空气阻力,则两小球( )
如图所示,两个小球从水平地面上方同一点O分别以初速度v1、v2水平抛出,落在地面上的位置分别是A和B,O′是O在地面上的竖直投影,且O′A:AB=2:3.若不计空气阻力,则两小球( )
 如图所示,两个小球从水平地面上方同一点O分别以初速度v1、v2水平抛出,落在地面上的位置分别是A和B,O′是O在地面上的竖直投影,且O′A:AB=2:3.若不计空气阻力,则两小球( )
如图所示,两个小球从水平地面上方同一点O分别以初速度v1、v2水平抛出,落在地面上的位置分别是A和B,O′是O在地面上的竖直投影,且O′A:AB=2:3.若不计空气阻力,则两小球( )| A. | 抛出的初速度大小之比为2:5 | |
| B. | 落地速度的大小之比为2:3 | |
| C. | 落地速度与水平地面夹角的正切值之比为1:3 | |
| D. | 通过的位移大小之比为1:$\sqrt{3}$ |
2. 如图所示,坐在火车上的乘客看到车外的房屋和树木以一定的速度在向后退,则他选择的参考系是( )
如图所示,坐在火车上的乘客看到车外的房屋和树木以一定的速度在向后退,则他选择的参考系是( )
 如图所示,坐在火车上的乘客看到车外的房屋和树木以一定的速度在向后退,则他选择的参考系是( )
如图所示,坐在火车上的乘客看到车外的房屋和树木以一定的速度在向后退,则他选择的参考系是( )| A. | 他乘坐的火车 | B. | 迎面驶来的火车 | C. | 路旁的房屋 | D. | 路旁的树木 |
20.下列说法中正确的是( )
| A. | 感应电流的磁场方向总是和回路中原磁场方向相反 | |
| B. | 感应电流的磁场总是阻止原磁通量的变化 | |
| C. | 感应电流的磁场方向有可能和原磁场方向相同,也可能和原磁场方向相反 | |
| D. | 当闭合回路中原磁场磁通量变化时,由于感应电流的阻碍作用,回路中总磁通量最后可能不变 |
