Question

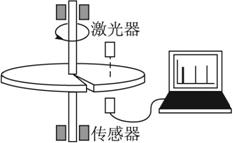
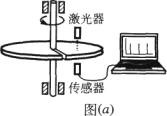
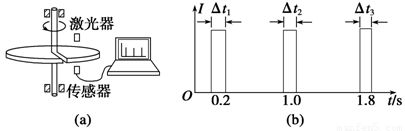
一水平放置的圆盘绕竖直固定的轴转动，在圆盘上沿半径开有一条宽度为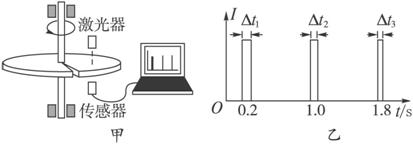2 mm的狭缝，将激光器与传感器上下对准，使二者接线与转动轴平行，分别置于圆盘的上下两侧，且可以同步地沿圆盘半径方向匀速移动.激光器连续向下发射激光束，在圆盘转动的过程中，当狭缝经过激光器与传感器之间时，传感器接收到一个激光信号，并将其输入计算机，经处理后画出相应图线，图18-5-2甲为该装置示意图，图18-5-2乙为所接收的光信号随时间变化的图线，横坐标表示时间，纵坐标表示接收到的激光信号强度，图中Δt₁=1.0×10^-3 s,Δt₂=0.8×10^-3 s.

图18-5-2

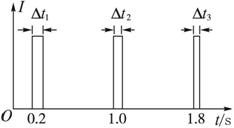
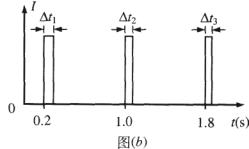
（1）利用图乙中的数据求1 s时圆盘转动的角速度；

（2）说明激光器和传感器沿半径移动的方向；

（3）求在图乙中第三个激光信号的宽度Δt₃.

Answer 1

解析：（1）由图线读得，转盘的转动周期为T=0.8 s

角速度为ω=rad/s=7.85 rad/s.

（2）由于脉冲宽度在逐渐变窄，表明光信号能通过狭缝的时间逐渐减小，即圆盘上的对应探测器所在位置的线速度逐渐增加，因此激光器和探测器沿半径由中心向边缘移动.

（3）设狭缝宽度为d，探测器接收到第i个脉冲时转动的距离为r_i，第i个脉冲的宽度为Δt _i，激光器和探测器沿半径的运动速度为v.

Δt_i=,

r₃-r₂=r₂-r₁=vT,

r₂-r₁=

r₃-r₂=

由以上各式解得Δt₃=≈0.67×10^-3 s.

答案：（1）7.85 rad/s  （2）激光器和探测器沿半径由中心向边缘移动  （3）0.67×10^-3 s