题目内容
9.近年来,中国航天事业实现了快速发展,取得了一系列新成就,中国人乘宇宙飞船探索月球将不再是梦想,当登月舱在月球表面着陆后,科研人圆在距月球表面高h处,以速度v0水平抛出一个小球,测得小球落地点与抛出点的水平距离为L,已知飞船绕贴近月球表面的圆形轨道运动一周所需的时间为T,试根据以上信息.求:(1)月球表面的重力加速度;
(2)月球的第一宇宙速度.
分析 (1)根据平抛运动的规律求月球表面的重力加速度;
(2)根据飞船的在月球表面重力提供向心力求出月球的半径,由第一宇宙速度的计算公式$v=\sqrt{gR}$,将g、R代入即可求出第一宇宙速度;
解答 解:(1)由平抛运动的规律:
水平方向:$L={v}_{0}^{\;}t$…①
竖直方向:$h=\frac{1}{2}g{t}_{\;}^{2}$…②
所以$g=\frac{2h{v}_{0}^{2}}{{L}_{\;}^{2}}$…③
(2)飞船围绕月球做匀速圆周运动,根据万有引力提供向心力$mg=m\frac{4{π}_{\;}^{2}}{{T}_{\;}^{2}}R$…④
得$R=\frac{g{T}_{\;}^{2}}{4{π}_{\;}^{2}}=\frac{{T}_{\;}^{2}}{4{π}_{\;}^{2}}×\frac{2h{v}_{0}^{2}}{{L}_{\;}^{2}}=\frac{h{v}_{0}^{2}{T}_{\;}^{2}}{2{π}_{\;}^{2}{L}_{\;}^{2}}$…⑤
月球的第一宇宙速度:$v=\sqrt{gR}=\sqrt{\frac{2h{v}_{0}^{2}}{{L}_{\;}^{2}}×\frac{h{v}_{0}^{2}{T}_{\;}^{2}}{2{π}_{\;}^{2}{L}_{\;}^{2}}}=\frac{hT{v}_{0}^{2}}{π{L}_{\;}^{2}}$…⑥
答:(1)月球表面的重力加速度$\frac{2h{v}_{0}^{2}}{{L}_{\;}^{2}}$;
(2)月球的第一宇宙速度$\frac{hT{v}_{0}^{2}}{{L}_{\;}^{2}}$
点评 解决本题的关键知道平抛运动在水平方向上和竖直方向上的运动规律,以及掌握万有引力提供向心力以及万有引力等于重力这两个理论的运用.

 新思维寒假作业系列答案
新思维寒假作业系列答案| A. | 物体在△t 时间内的平均速度 | |
| B. | 物体在△t 时间内速度的增加量 | |
| C. | 物体经过△t 时间内的位移中点时的即时速度 | |
| D. | 物体经过△t 时间内中间时刻的即时速度 |
| A. | 能量是守恒的,所以根本不用担心“能量危机” | |
| B. | 虽然能量时守恒的,但也要节约能源 | |
| C. | 跳伞运动员匀速下降的过程中机械能守恒 | |
| D. | 若两个物体的重心等高,则质量大的物体重力势能一定大 |
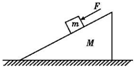 如图所示,一质量为m的物体恰能在质量为M的斜面上匀速下滑,斜面保持静止.现用一沿斜面向下的外力F推此物体,使物体加速下滑;设此过程中斜面受到地面的摩擦力为f,支持力为N,则下列说法正确的是( )
如图所示,一质量为m的物体恰能在质量为M的斜面上匀速下滑,斜面保持静止.现用一沿斜面向下的外力F推此物体,使物体加速下滑;设此过程中斜面受到地面的摩擦力为f,支持力为N,则下列说法正确的是( )| A. | f为零,N=(m+M)g | B. | f不为零,N=(m+M)g | C. | f不为零,N>(m+M)g | D. | f为零,N<(m+M)g |
 如图所示,球带正电q,单摆摆长为 l,当地的重力加速度为g,其最大摆角为θ,整个装置处于垂直纸面向里,强度为B的匀强磁场中.当摆球从如图所示最大摆角处运动到摆线竖直的过程中,下列说法中不正确的是( )
如图所示,球带正电q,单摆摆长为 l,当地的重力加速度为g,其最大摆角为θ,整个装置处于垂直纸面向里,强度为B的匀强磁场中.当摆球从如图所示最大摆角处运动到摆线竖直的过程中,下列说法中不正确的是( )| A. | 在此过程中,重力的冲量为$\frac{π}{2}$m$\sqrt{lg}$,方向竖直向下 | |
| B. | 在此过程中,只有重力做功,所以小球的机械能守恒 | |
| C. | 在此过程中,合力对小球的冲量大小为m$\sqrt{2gl(1-cosθ)}$ | |
| D. | 当摆线摆到竖直位置时,线的拉力T=mg+qB$\sqrt{2gl(1-cosθ)}$ |
| A. | 0 | B. | 30N,水平向左 | C. | 15N,水平向右 | D. | 15N,水平向左 |
| A. | 卫星的动能 | B. | 卫星所受地球的万有引力 | ||
| C. | 卫星的角速度 | D. | 卫星做圆周运动的向心加速度 |
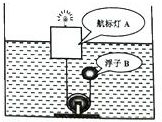 科技节中,小宇同学用泡沫塑料、灯泡和滑轮等物件制作了一个航标灯模型. 如图所示,在容器底部固定一滑轮,并用细绳将柱形航标灯A和浮子B相连.其原理是:当水位上升时,浮子B下降;水位下降时,浮子B上升,使航标灯A静止时浸入水中的深度始终保持h=0.05m.己知航标灯A总质量m1=0.3kg,底面积S=8.0×10-3 m2,浮子B的密度ρ=$\frac{1}{3}$×l03kg/m3 (不计绳重和滑轮之间的摩擦).求:
科技节中,小宇同学用泡沫塑料、灯泡和滑轮等物件制作了一个航标灯模型. 如图所示,在容器底部固定一滑轮,并用细绳将柱形航标灯A和浮子B相连.其原理是:当水位上升时,浮子B下降;水位下降时,浮子B上升,使航标灯A静止时浸入水中的深度始终保持h=0.05m.己知航标灯A总质量m1=0.3kg,底面积S=8.0×10-3 m2,浮子B的密度ρ=$\frac{1}{3}$×l03kg/m3 (不计绳重和滑轮之间的摩擦).求: