题目内容

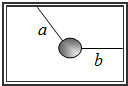如图所示，矩形盒内用两根细线固定一个质量为m=1.0kg的均匀小球，a线与水平方向成53°角，b线水平．两根细线所能承受的最大拉力都是F_m=15N．当该系统沿竖直方向加速上升时，为保证细线不被拉断，加速度可取的最大值是m/s²；当该系统沿水平方向向右匀加速运动时，为保证细线不被拉断，加速度可取的最大值是m/s²．（取g=10m/s²）

2 7.5
分析：对小球受力分析，通过细绳的最大拉力，根据牛顿第二定律求出加速度的最大值．
解答：当系统沿竖直方向加速上升时，有：F_msin53°-mg=ma_m，解得 $\text{[math]}$ ．
当系统沿水平方向匀加速运动时，水平方向上有：F_m-T_acos53°=ma_m，竖直方向上有：T_asin53°=mg，联立两式解得 $\text{[math]}$ ．
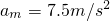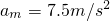故答案为：2，7.5．
点评：解决本题的关键能够正确地受力分析，运用牛顿第二定律进行求解．

练习册系列答案

相关题目

如图所示，矩形盒内用两根细线固定一个质量为m=1.0kg的均匀小球，a线与水平方向成53°角，b线水平．两根细线所能承受的最大拉力都是F_m=15N．当该系统沿竖直方向加速上升时，为保证细线不被拉断，加速度可取的最大值是

m/s²；当该系统沿水平方向向右匀加速运动时，为保证细线不被拉断，加速度可取的最大值是

7.5

m/s²．（取g=10m/s²）

如图所示，矩形盒内用两根细线固定一个质量为m=1.0kg的均匀小球，a线与水平方向成53°角，b线水平。两根细线所能承受的最大拉力都是F_m=15N。当该系统沿竖直方向匀加速上升时，为保证细线不被拉断，加速度可取的最大值是_____m/s²；当该系统沿水平方向向右匀加速运动时，为保证细线不被拉断，加速度可取的最大值是_____m/s²。（取g=10m/s²）

如图所示，矩形盒内用两根细线固定一个质量为m=1.0kg的均匀小球，a线与水平方向成53°角，b线水平．两根细线所能承受的最大拉力都是F_m=15N．当该系统沿竖直方向加速上升时，为保证细线不被拉断，加速度可取的最大值是 m/s²；当该系统沿水平方向向右匀加速运动时，为保证细线不被拉断，加速度可取的最大值是 m/s²．（取g=10m/s²）

试题分类