题目内容
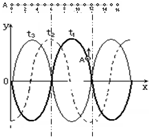
 图A中表示一条均匀细绳,0、1、2、…表示绳上一系列等距离的质点,由0到16点的长度是2.4m,一列简谐波沿此绳传播,绳上A点的振动方向如图所示,在t1=0时刻、t2=11s时刻、t3=22s时刻的波形图如图所示,试求:
图A中表示一条均匀细绳,0、1、2、…表示绳上一系列等距离的质点,由0到16点的长度是2.4m,一列简谐波沿此绳传播,绳上A点的振动方向如图所示,在t1=0时刻、t2=11s时刻、t3=22s时刻的波形图如图所示,试求:(1)此波的波长及波的传播方向
(2)此波在绳中的最小传播速度.
分析:(1)根据波动图象与绳子的长度可确定波的波长,并由质点振动方向来确定波的传播方向.
(2)根据v=
,可知当周期越长时,则波速越小.因此由波的周期性,从而确定最长周期,即可求解.
(2)根据v=
| λ |
| T |
解答:解:(1)由0到16点的长度是2.4m,而由0到10点的长度是波长,所以波长λ=1.8m,
根据绳上A点的振动方向如图所示,结合“逆向描波”可知,波向x轴正方向传播.
(2)在一个周期内,从t1时刻到t2时刻,从t1时刻t3时刻对应的波动图象如图,则有:
t2-t1=(n+
)T(n=0、1、2…)
所以周期为
T=
(n=0、1、2…)
由图知波长为λ=1.8m
所以波速为
v=
=
(4n+3)(n=0、1、2…)
当n=0时,波速最小,即最小波速为0.123m/s.
t3-t1=(n+
)T(n=0、1、2…)
所以周期为
T=
(n=0、1、2…)
由图知波长为λ=1.8m
所以波速为
v=
=
(2n+3)(n=0、1、2…)
当n=0时,波速最小,即最小波速为0.123m/s.
答:(1)波长为1.8m,波向右传播.
(2)此波的最小传播速度为0.123m/s
根据绳上A点的振动方向如图所示,结合“逆向描波”可知,波向x轴正方向传播.
(2)在一个周期内,从t1时刻到t2时刻,从t1时刻t3时刻对应的波动图象如图,则有:
t2-t1=(n+
| 3 |
| 4 |
所以周期为
T=
| 4×11 |
| 4n+3 |
由图知波长为λ=1.8m
所以波速为
v=
| λ |
| T |
| 1.8 |
| 44 |
当n=0时,波速最小,即最小波速为0.123m/s.
t3-t1=(n+
| 3 |
| 2 |
所以周期为
T=
| 2×22 |
| 2n+3 |
由图知波长为λ=1.8m
所以波速为
v=
| λ |
| T |
| 1.8 |
| 44 |
当n=0时,波速最小,即最小波速为0.123m/s.
答:(1)波长为1.8m,波向右传播.
(2)此波的最小传播速度为0.123m/s
点评:根据波的周期性,得到t2-t1与周期的关系,得出周期的通项.由图读出波长,求出波速的通项,再由数学知识求出波速的最小值.

练习册系列答案
相关题目