题目内容
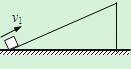
【题目】如下图所示,在水平匀速运动的传送带的左端(P点),轻放一质量为m=1kg的物块,物块随传送带运动到A点后水平抛出,恰好无碰撞的沿圆弧切线从B点进入竖直光滑圆弧轨道下滑.B、D为圆弧的两端点,其连线水平.已知圆弧半径R=1.0m,圆弧对应的圆心角θ=106°,轨道最低点为C,A点距水平面的高度h=0.8m.(g取10m/s2,sin53°=0.8,cos53°=0.6)求:
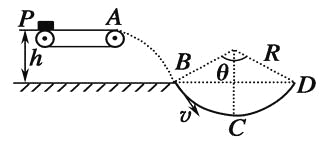
(1)物块离开A点时水平初速度的大小;
(2)物块经过C点时对轨道压力的大小;
(3)设物块与传送带间的动摩擦因数为0.3,传送带的速度为5m/s,求PA间的距离.
【答案】(1)3m/s (2)43N (3)1.5m
【解析】
(1)物块运动至B点时,合速度v的方向与水平速度v0的方向成53°
角,有![]() (1分) 又
(1分) 又![]()
联立以上两式,代入数据得![]()
(2)物块由B运动至C的过程中应用动能定理得:
![]()
vB=5![]()
在C点有:![]()
联立上述两式,可得F="43N "
(3)物块运动的加速度a=3m/s2
运动至A点所需的时间为![]()
距离![]()

【题目】某同学在“研究匀变速直线运动”的实验中,用打点计时器记录了被小车拖动的纸带的运动情况,在纸带上确定出A、B、C、D、E、F、G共7个计数点,其相邻两点间的距离如图甲所示,每两个相邻的计数点之间的时间间隔均为0.10s。
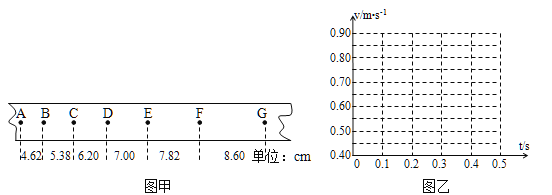
(1)试根据纸带上各个计数点间的距离,计算打下B、C、D、E、F五个点时小车的瞬时速度,请将D点的速度值填在下面的表格内(保留到小数点后两位);
计数点序号 | B | C | D | E | F |
计数点对应的时刻t/s | 0.1 | 0.2 | 0.3 | 0.4 | 0.5 |
通过计数点时小车的速度v/ms﹣1 | 0.50 | 0.58 | 0.74 | 0.82 |
(2)以A点为计时零点,将B、C、D、E、F各个时刻的瞬时速度标在如图乙所示的坐标纸上,并画出小车的瞬时速度v随时间t变化的关系图线;
(3)根据第(2)问中画出的v﹣t图线,求出小车运动的加速度大小a= m/s2(保留三位有效数字)。