题目内容
13. 如图所示,一个电荷量为e、质量为m的带电粒子,以初速度v0从偏转电场的极板左端中央沿垂直电场方向射入匀强偏转电场,偏转后通过位于下极板的小孔S离开电场,进入范围足够大、上端和左端有理想边界、磁感应强度为B、方向垂直纸面向外的匀强磁场,磁场区域的上端以偏转电场的下极板为边界,磁场的左边界MN与偏转电场的下极板垂直,且MN与小孔S左边缘相交于M点.已知带电粒子通过小孔S时的速度方向与下极板的夹角成θ=45°,整个装置处于真空中,粒子所受重力、小孔S的大小及偏转电场的边缘效应均可忽略不计.
如图所示,一个电荷量为e、质量为m的带电粒子,以初速度v0从偏转电场的极板左端中央沿垂直电场方向射入匀强偏转电场,偏转后通过位于下极板的小孔S离开电场,进入范围足够大、上端和左端有理想边界、磁感应强度为B、方向垂直纸面向外的匀强磁场,磁场区域的上端以偏转电场的下极板为边界,磁场的左边界MN与偏转电场的下极板垂直,且MN与小孔S左边缘相交于M点.已知带电粒子通过小孔S时的速度方向与下极板的夹角成θ=45°,整个装置处于真空中,粒子所受重力、小孔S的大小及偏转电场的边缘效应均可忽略不计.(1)求偏转电场两极板间的电压U;
(2)带电粒子从磁场的左边界MN的S1点飞出,求M点与S1点间的距离L.
分析 (1)粒子在偏转电场中做类平抛运动,根据题意求出粒子离开电场时的竖直分速度,然后应用动能定理可以求出偏转电场间的电压.
(2)粒子在磁场中做匀速圆周运动,洛伦兹力提供向心力,由牛顿第二定律求出粒子做圆周运动的轨道半径,然后求出M点与S1点间的距离.
解答 解:(1)粒子在偏转电场中做类平抛运动,由题意可知,带电粒子通过小孔S时的速度方向与下极板的夹角成θ=45°
粒子离开电场时竖直分速度:vy=v0tan45°=v0,
粒子在偏转电场中运动过程中,由动能定理得:
e•$\frac{U}{2}$=$\frac{1}{2}$mvy2-0,
解得:U=$\frac{m{v}_{0}^{2}}{e}$;
(2)粒子进入磁场时的速度:v=$\frac{{v}_{0}}{cos45°}$=$\sqrt{2}$v0,
粒子在磁场中做匀速圆周运动,洛伦兹力提供向心力,由牛顿第二定律得:
evB=m$\frac{{v}^{2}}{r}$,
解得:r=$\frac{\sqrt{2}m{v}_{0}}{eB}$,
M点与S1点间的距离:L=2rcos45°=$\frac{2m{v}_{0}}{eB}$;
答:(1)偏转电场两极板间的电压U为$\frac{m{v}_{0}^{2}}{e}$;
(2)带电粒子从磁场的左边界MN的S1点飞出,M点与S1点间的距离L为$\frac{2m{v}_{0}}{eB}$.
点评 本题考查了粒子在电场与磁场中的运动,分析清楚粒子运动过程是正确解题的前提与关键,应用运动的合成与分解知识,应用动能定理、牛顿第二定律即可解题,解题时注意几何知识的应用;对于粒子在匀强磁场中的圆周运动,关键找出圆周运动所需的向心力,列出等式解决问题,对于粒子垂直射入平行板电容器中的问题,要知道粒子做类平抛运动,能根据平抛运动基本公式求解,难度较大.

 名校课堂系列答案
名校课堂系列答案 如图所示,重物A被绕过小滑轮P的细线所悬挂,小滑轮P被一根细线系于天花板上的O 点.质量为5kg的物体B放在粗糙的水平桌面上,与水平面的动摩擦因数为μ=0.5.O′是三根线的结点,细绳bO′水平拉着B物体,aO′、bO′与cO′夹角如图所示.细绳、小滑轮的重力和细线与滑轮间的摩擦力均可忽略,整个装置处于静止状态.若悬挂小滑轮的细线OP的张力是20$\sqrt{3}$N,则下列说法中正确的是:(取:g=10m/s2)( )
如图所示,重物A被绕过小滑轮P的细线所悬挂,小滑轮P被一根细线系于天花板上的O 点.质量为5kg的物体B放在粗糙的水平桌面上,与水平面的动摩擦因数为μ=0.5.O′是三根线的结点,细绳bO′水平拉着B物体,aO′、bO′与cO′夹角如图所示.细绳、小滑轮的重力和细线与滑轮间的摩擦力均可忽略,整个装置处于静止状态.若悬挂小滑轮的细线OP的张力是20$\sqrt{3}$N,则下列说法中正确的是:(取:g=10m/s2)( )| A. | 重物A的质量为3kg | |
| B. | 桌面对B物体的摩擦力为10$\sqrt{3}$N | |
| C. | 重物C的质量为2kg | |
| D. | 若改变A、C两物体的质量,在保证结点O′位置不变的前提下为使系统平衡,A物体重量不超过$\frac{{50\sqrt{3}}}{3}N$ |
| A. | 相遇时a、b两球速度方向相同 | B. | 相遇后b球再经过$\frac{1}{2}$t到达最高点 | ||
| C. | 相遇后b球再经过$\frac{3}{2}$t回到地面 | D. | $\frac{H}{h}$=$\frac{3}{2}$ |


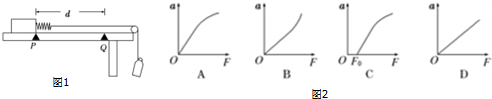
 如图所示,q1、q2、q3分别表示在一条直线上的三个点电荷,且每个电荷都处于平衡状态.(只考虑它们间的静电力)求:
如图所示,q1、q2、q3分别表示在一条直线上的三个点电荷,且每个电荷都处于平衡状态.(只考虑它们间的静电力)求: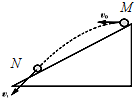 2007年10月24日,中国首颗探月卫星“嫦娥一号”从西昌卫星发射中心发射升空,11月26日,中国第一幅月图完美亮相,中国首次月球探测工程取得圆满成功.我国将在2017年前后发射一颗返回式月球软着陆器,进行首次月球样品自动取样并安全返回地球.假设探月宇航员站在月球表面一斜坡上的M点,并沿水平方向以初速度v0抛出一个质量为m的小球,测得小球经时间t落到斜坡上另一点N,斜面的倾角为α,已知月球半径为R,月球的质量分布均匀,万有引力常量为G,求:
2007年10月24日,中国首颗探月卫星“嫦娥一号”从西昌卫星发射中心发射升空,11月26日,中国第一幅月图完美亮相,中国首次月球探测工程取得圆满成功.我国将在2017年前后发射一颗返回式月球软着陆器,进行首次月球样品自动取样并安全返回地球.假设探月宇航员站在月球表面一斜坡上的M点,并沿水平方向以初速度v0抛出一个质量为m的小球,测得小球经时间t落到斜坡上另一点N,斜面的倾角为α,已知月球半径为R,月球的质量分布均匀,万有引力常量为G,求: