Question

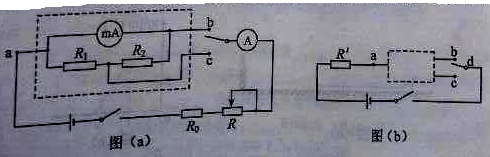
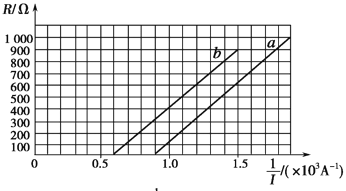
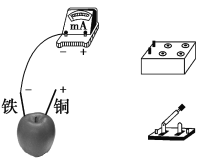
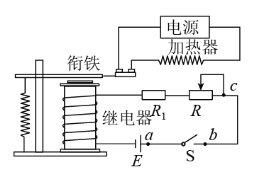
【题目】如图所示，电源电动势E＝27 V，内阻r＝2 Ω，固定电阻R2＝4 Ω，R1为光敏电阻．C为平行板电容器，其电容C＝3pF，虚线到两极板距离相等，极板长L＝0.2 m，间距d＝1.0×10－2 m．P为一圆盘，由形状相同透光率不同的二个扇形a、b构成，它可绕AA′轴转动．当细光束通过扇形a、b照射光敏电阻R1时，R1的阻值分别为12 Ω、3 Ω.有带电量为q＝－1.0×10－4 C微粒沿图中虚线以速度v0＝10 m/s连续射入C的电场中．假设照在R1上的光强发生变化时R1阻值立即有相应的改变．重力加速度为g＝10 m/s2.

(1)求细光束通过a照射到R1上时，电容器所带的电量；

(2)细光束通过a照射到R1上时，带电微粒刚好沿虚线匀速运动，求细光束通过b照射到R1上时带电微粒能否从C的电场中射出．

Answer 1

【答案】（1）（2）带电粒子能从C的电场中射出

【解析】

由闭合电路欧姆定律求出电路中电流，再由欧姆定律求出电容器的电压，即可由Q=CU求其电量；细光束通过a照射到R1上时，带电微粒刚好沿虚线匀速运动，电场力与重力二力平衡．细光束通过b照射到R1上时，根据牛顿第二定律求粒子的加速度，由类平抛运动分位移规律分析微粒能否从C的电场中射出．

（1）由闭合电路欧姆定律，得

又电容器板间电压，得UC=6V

设电容器的电量为Q，则Q=CUC解得

（2）细光束通过a照射时，带电微粒刚好沿虚线匀速运动，则有

解得

细光束通过b照射时，同理可得

由牛顿第二定律，得 解得

微粒做类平抛运动，得，

解得， 所以带电粒子能从C的电场中射出．