题目内容
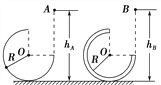
【题目】如图所示，竖直面内半径为R的光滑半圆形轨道与水平光滑轨道相切于D点。a、b、c三个物体由水平部分分别向半环滑去，最后重新落回到水平面上时的落点到切点D的距离依次为AD＜2R，BD＝2R，CD＞2R。设三个物体离开半圆形轨道在空中飞行时间依次为ta、tb、tc，三个物体到达地面的动能分别为Ea、Eb、Ec，则下面判断正确的是（ ）
A. Ea＝Eb B. Ec＝Ea C. tb＝tc D. ta＝tb
【答案】C
【解析】物体若从圆环最高点离开半环在空中做平抛运动，竖直方向上做自由落体运动，则有： 
得： 
物体恰好到达圆环最高点时，有： 
则通过圆轨道最高点时最小速度为： 
所以物体从圆环最高点离开后平抛运动的水平位移最小值为： 
由题知：AD＜2R，BD=2R，CD＞2R，说明b.c通过最高点做平抛运动，a没有到达最高点，则知
， 
，对于a.b两球，通过D点时，a的速度比b的小，由机械能守恒可得： 
．对于b.c两球，由
知，t相同，c的水平位移大，通过圆轨道最高点时的速度大，由机械能守恒定律可知， 
．故C正确
综上所述本题答案是：C
练习册系列答案
相关题目
