题目内容
11.在圆轨道上质量为m的人造地球卫星,它到地面的距离等于地球半径R,地面上的重力加速度为g,则( )| A. | 卫星运动的速度为$\sqrt{2Rg}$ | B. | 卫星运动的周期为4π$\sqrt{\frac{2R}{g}}$ | ||
| C. | 卫星运动的加速度为$\frac{1}{2}$g | D. | 卫星的角速度为$\frac{1}{4}$mRg |
分析 人造地球卫星绕地球做匀速圆周运动,根据人造卫星的万有引力等于向心力,列式求出线速度、角速度、周期和向心力的表达式,再结合地球表面重力加速度的公式解题.
解答 解:设卫星的质量为m、轨道半径为r=R+R=2R,地球质量为M,人造卫星绕地球做匀速圆周运动,根据万有引力提供向心力;
在地球表面的物体受到的重力等于万有引力,即:G$\frac{Mm′}{{R}^{2}}$=mg,则:GM=gR2;
A、由牛顿第二定律得:G$\frac{Mm}{(2R)^{2}}$=m$\frac{{v}^{2}}{2R}$,解得:v=$\sqrt{\frac{gR}{2}}$,故A错误;
B、由牛顿第二定律得:G$\frac{Mm}{(2R)^{2}}$=m$(\frac{2π}{T})^{2}$•2R,解得:T=4π$\sqrt{\frac{2R}{g}}$,故B正确;
C、由牛顿第二定律得:G$\frac{Mm}{(2R)^{2}}$=ma,解得:a=$\frac{1}{4}$g,故C错误;
D、由牛顿第二定律得:G$\frac{Mm}{(2R)^{2}}$=mω2•2R,解得:ω=$\sqrt{\frac{g}{8R}}$,故D错误;
故选:B.
点评 本题考查了万有引力定律的应用,解题的关键是根据人造卫星的万有引力等于向心力,以及地球表面重力等于万有引力列两个方程求解.

练习册系列答案
 课堂练加测系列答案
课堂练加测系列答案 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案
相关题目
3. 如图所示,地面上竖直放一根轻弹簧,其下端和地面固定连接,一物体从弹簧正上方距弹簧一定高度处自由下落,则( )
如图所示,地面上竖直放一根轻弹簧,其下端和地面固定连接,一物体从弹簧正上方距弹簧一定高度处自由下落,则( )
 如图所示,地面上竖直放一根轻弹簧,其下端和地面固定连接,一物体从弹簧正上方距弹簧一定高度处自由下落,则( )
如图所示,地面上竖直放一根轻弹簧,其下端和地面固定连接,一物体从弹簧正上方距弹簧一定高度处自由下落,则( )| A. | 物体和弹簧接触时,物体的动能最大 | |
| B. | 与弹簧接触的整个过程,物体的动能和弹簧弹性势能的和不断增加 | |
| C. | 与弹簧接触的整个过程,物体的动能与弹簧弹性势能的和先增加后减小 | |
| D. | 物体在反弹阶段,动能一直增加直到物体脱离弹簧为止 |
20.图甲、图乙分别表示两种电压的波形,其中图甲所示电压按正弦规律变化.下列说法不正确的是( )


| A. | 图甲表示交流电,图乙表示直流电 | |
| B. | 两种电压的有效值相等 | |
| C. | 图甲所示电压的瞬时值表达式为u=311sin100πtV | |
| D. | 图乙所示电压的瞬时值表达式为u=311sin100πtV |
18.某行星的质量约是地球的6倍,其表面重力加速度是地球表面重力加速度的1.6倍,则该行星的半径和地球的半径之比为( )
| A. | $\frac{{\sqrt{15}}}{2}$ | B. | 15:4 | C. | $\frac{2}{{\sqrt{15}}}$ | D. | 4:15 |



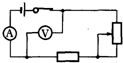
 用游标为20分度的卡尺(测量值可准确到0.05mm)测量某圆筒的内径时卡尺上的示数如图所示,此示数为20.40mm.
用游标为20分度的卡尺(测量值可准确到0.05mm)测量某圆筒的内径时卡尺上的示数如图所示,此示数为20.40mm.