题目内容
1. 如图所示,一质量为4m、半径为R的球形空腔容器静止在光滑的水平地面上,另一质量为m、可视为质点的小球从球心O等高的A点由静止释放,当小球运动到最低点B时,小球的水平位移大小为$\frac{4}{5}$R,空腔容器的位移大小为$\frac{1}{5}$R.(球形空腔容器的壁厚不计)
如图所示,一质量为4m、半径为R的球形空腔容器静止在光滑的水平地面上,另一质量为m、可视为质点的小球从球心O等高的A点由静止释放,当小球运动到最低点B时,小球的水平位移大小为$\frac{4}{5}$R,空腔容器的位移大小为$\frac{1}{5}$R.(球形空腔容器的壁厚不计)
分析 小球与空腔组成的系统在水平方向动量守恒,应用动量守恒定律即可求出小球与空腔的位移.
解答 解:小球与空腔组成的系统在水平方向动量守恒,
以向右为正方向,设空腔的位移为x,
在水平方向,由动量守恒定律得:
mv小球-4mv空腔=0,
m$\frac{R-x}{t}$-4m$\frac{x}{t}$=0,
解得:x=$\frac{1}{5}$R,小球的位移为:R-x=$\frac{4}{5}$R;
故答案为:$\frac{4}{5}$R;$\frac{1}{5}$R.
点评 本题考查了求小球与空腔的水平位移,分析清楚运动过程、应用动量守恒定律即可正确解题.

练习册系列答案
 期末集结号系列答案
期末集结号系列答案
相关题目
11.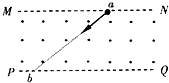 如图所示,在MN、PQ间同时存在匀强磁场和匀强电场,方向垂直纸面水平向外,电场在图中没有标出.一带电小球从a点射入场区,并在竖直面内沿直线运动至b点,则小球( )
如图所示,在MN、PQ间同时存在匀强磁场和匀强电场,方向垂直纸面水平向外,电场在图中没有标出.一带电小球从a点射入场区,并在竖直面内沿直线运动至b点,则小球( )
 如图所示,在MN、PQ间同时存在匀强磁场和匀强电场,方向垂直纸面水平向外,电场在图中没有标出.一带电小球从a点射入场区,并在竖直面内沿直线运动至b点,则小球( )
如图所示,在MN、PQ间同时存在匀强磁场和匀强电场,方向垂直纸面水平向外,电场在图中没有标出.一带电小球从a点射入场区,并在竖直面内沿直线运动至b点,则小球( )| A. | 一定带正电 | B. | 受到电场力的方向一定水平向右 | ||
| C. | 从a到b过程,克服电场力做功 | D. | 从a到b过程中可能做匀加速运动 |
12.有关分子的热运动和内能,下列说法正确的是( )
| A. | 一定质量的气体,温度不变,分子的平均动能不变 | |
| B. | 物体的内能是物体的动能和重力势能的总和 | |
| C. | 布朗运动是由悬浮在液体中的微粒之间的相互碰撞引起的 | |
| D. | 外界对物体做功,物体的内能可能减少 |
6.磁悬浮列车从静止开始沿着平直轨道做匀加速运动,经过1250m的路程加速,速度达到50m/s.已知整个列车的质量是1.0×105kg,如果不计阻力,在这个过程中,机车牵引力的最大功率为( )
| A. | 5.0×106W | B. | 2.0×106W | C. | 5.0×108W | D. | 2.3×107W |
10.关于扩散现象,下来说法正确的是( )
| A. | 温度越高,扩散进行得越快 | |
| B. | 扩散现象是不同物质间的一种化学反应 | |
| C. | 扩散现象是由物质分子无规则运动产生的 | |
| D. | 扩散现象在气体、液体和固体中都能发生 | |
| E. | 液体中的扩散现象是由于液体的对流形成的 |
20.下列说法中正确的是( )
| A. | 光的双缝干涉实验中,若仅将入射光从红光改为紫光,则相邻亮条纹间距一定变大 | |
| B. | 在受迫振动中,驱动力的频率不一定等于物体的固有频率 | |
| C. | 宇航员驾驶宇宙飞船以接近光速经过地球时,地球上的人观察到飞船上的时钟变快 | |
| D. | 液晶显示器应用光的偏振制成 | |
| E. | 光导纤维传播光信号利用了光的全反射原理 |
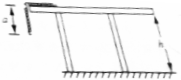 如图所示,在光滑的水平桌面上,放置一条长为l的均匀不锈钢链条,链条沿桌子边缘下垂部分的长度为a,由于受到某一干扰,链条由此位置从静止开始滑落,求当链条刚好全部滑出桌面瞬间链条的速度.(桌面离地面的高度h大于链条的长度l)
如图所示,在光滑的水平桌面上,放置一条长为l的均匀不锈钢链条,链条沿桌子边缘下垂部分的长度为a,由于受到某一干扰,链条由此位置从静止开始滑落,求当链条刚好全部滑出桌面瞬间链条的速度.(桌面离地面的高度h大于链条的长度l)