题目内容
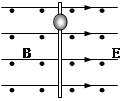
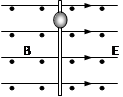
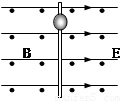
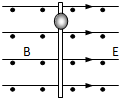 如图所示,竖直绝缘杆处于彼此垂直,大小分别为E和B的匀强电磁场中,电场方向水平向右,磁场方向垂直纸面向外,一个质量为m,带正电为q的小球从静止开始沿杆下滑,且与杆的动摩擦因数为μ,问:
如图所示,竖直绝缘杆处于彼此垂直,大小分别为E和B的匀强电磁场中,电场方向水平向右,磁场方向垂直纸面向外,一个质量为m,带正电为q的小球从静止开始沿杆下滑,且与杆的动摩擦因数为μ,问:(1)小球速度多大时,小球加速度最大?是多少?
(2)小球下滑的最大速度是多少?
分析:(1)小球受重力、摩擦力(可能有)、弹力(可能有)、向左的洛伦兹力、向右的电场力,当洛伦兹力等于电场力时,合力等于重力,加速度最大;
(2)当洛伦兹力大于电场力,且滑动摩擦力与重力平衡时,速度最大.
(2)当洛伦兹力大于电场力,且滑动摩擦力与重力平衡时,速度最大.
解答:解:(1)小球受重力、摩擦力(可能有)、弹力(可能有)、向左的洛伦兹力、向右的电场力,当洛伦兹力等于电场力时,合力等于重力,加速度最大,故:
mg=ma
qE=qvB
解得:
a=g
v=
(2)当洛伦兹力大于电场力,且滑动摩擦力与重力平衡时,速度最大,根据平衡条件,有
qvB-qE-N=0
f=μN=mg
解得:
v=
答:(1)小球速度为
时,小球加速度最大,是g;
(2)小球下滑的最大速度是为
.
mg=ma
qE=qvB
解得:
a=g
v=
| E |
| B |
(2)当洛伦兹力大于电场力,且滑动摩擦力与重力平衡时,速度最大,根据平衡条件,有
qvB-qE-N=0
f=μN=mg
解得:
v=
| mg+μqE |
| μqB |
答:(1)小球速度为
| E |
| B |
(2)小球下滑的最大速度是为
| mg+μqE |
| μqB |
点评:本题关键明确小球的运动情况,先做加速度增加的加速运动,然后做加速度减小的加速运动,当加速度减为零时,速度最大.

练习册系列答案
相关题目