题目内容
1. 某介质中有一列简谐波,t=0时刻的波形如图中实线所示,若波向右传播,零时刻刚好传到B点,且再经过0.6s,P点也开始起振,求:
某介质中有一列简谐波,t=0时刻的波形如图中实线所示,若波向右传播,零时刻刚好传到B点,且再经过0.6s,P点也开始起振,求:(1)从t=0时刻起到P点第一次达到波峰的过程中,O点对平衡位置的位移y0,及其经过的路程.
(2)若该列波的传播速度大小为20m/s,且波形中由实线变成虚线需要经历0.525s时间,试推断该列波的传播方向.
分析 (1)波向右匀速传播,根据题意知道波传播距离为x=6m时,用时为t=0.6s,求出波速,由图读出波长,求出周期.再根据时间和周期的关系,分析求解质点O通过的路程,再确定O的位置,得到位移.
(2)由波速和时间求出波传播的距离,研究与波长的关系,根据波形的平移确定波的传播方向.
解答 解:(1)由图象可知,波长λ=2m;
当波向右传播时,点B的起振方向沿-y方向,包括P点在内的各质点的起振方向均沿-y方向.
据题得波速 v=$\frac{{x}_{PB}}{t}$=$\frac{7-1}{0.6}$=10m/s
由v=$\frac{λ}{T}$得,周期T=$\frac{λ}{v}$=$\frac{2}{10}$s=0.2s.
从t=0时刻起到P点第一次达到波峰的过程经历时间为 t′=t+$\frac{3}{4}$T=0.6+$\frac{3}{4}×$0.2=0.75s
因为 $\frac{t′}{T}$=$\frac{0.75}{0.2}$=3$\frac{3}{4}$=$\frac{15}{4}$,所以在这段时间内质点O通过的路程为 S=$\frac{15}{4}$×4A=15×2cm=30cm
P点第一次达到波峰时O点到达波谷,其对平衡位置的位移y0=-2cm
(2)若波速v=20m/s,时间t=0.525s,则波沿x轴方向传播的距离为:
x=vt=20×0.525m=10.5m=(5+$\frac{1}{4}$)λ
根据波形的平移可知,波沿x轴负方向传播.
答:(1)从t=0时刻起到P点第一次达到波峰的过程中,O点对平衡位置的位移y0是-2cm,经过的路程是30cm;
(2)该列波的传播方向沿x轴负方向.
点评 本题是知道两个时刻的波形研究波传播的距离、波速、周期的问题.第(2)问可以根据波的周期性,运用数学知识列出波传播距离的通项式,再确定波的传播方向.

 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案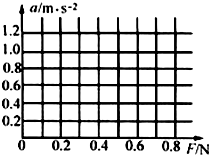 在探究加速度与力的关系中,保持小车质量不变,得到如表所示的一组实验数据:
在探究加速度与力的关系中,保持小车质量不变,得到如表所示的一组实验数据:| F/N | 0.20 | 0.30 | 0.40 | 0.50 | 0.60 | 0.70 |
| a/m•s-2 | 0.22 | 0.38 | 0.56 | 0.80 | 0.96 | 1.16 |
(2)从a-F关系图中可以判断实验操作中存在的问题是未平衡摩擦力或平衡摩擦力不足;
(3)从图中求出小车的质量为0.57kg.

| 计数点 | A | B | C | D | E | F |
| h/cm | 6.9 | 9.47 | 12.40 | 15.71 | 19.41 | 23.49 |
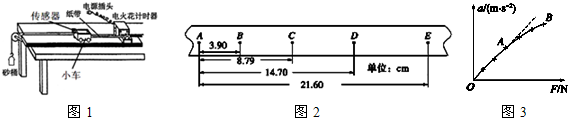
(2)下面列举了该实验的几个操作步骤:
A.按照图示的装置安装器件
B.将打点计时器接到电源的“直流输出”上;
C.用天平测出重锤的质量
D.释放纸带,立即接通电源开关打出一条纸带;
E.测量纸带上某些点间的距离;
F.根据测量的结果计算重锤下落过程中减少的重力势能是否等于增加的动能
其中没有必要进行的或者操作不当的步骤是BCD(填选项对应的字母)
(3)打点计时器的频率为50Hz,则计时器打下C点时,重物的速度大小为1.56m/s;
(4)计数点C、D、E与O点之间的距离分别用hC、hD、hE表示,打点计时器的打点周期用T表示,若重物质量为m,重力加速度为g,则从O到D重物动能的增加量△Ek=$\frac{{m{{({h_E}-{h_C})}^2}}}{{8{T^2}}}$;O到D重物重力势能的减少量△EP=mghD(△Ek、△EP均用hC、hD、hE、T、m、g符号表示).
①指针稳定后,线圈受到螺旋弹簧的力矩与线圈受到的磁力矩方向是相反的
②通电线圈中的电流越大,电流表指针偏转的角度也越大
③在线圈转动的范围内,各处的磁场都是匀强磁场
④在线圈转动的范围内,线圈所受磁力大小与电流大小有关,而与所处位置无关.
| A. | ①② | B. | ③④ | C. | ①②④ | D. | ①②③④ |
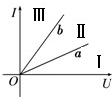 如图所示,a、b分别表示由相同材料制成的两条长度相同、粗细均匀电阻丝的伏安特性曲线,下列判断中正确的是( )
如图所示,a、b分别表示由相同材料制成的两条长度相同、粗细均匀电阻丝的伏安特性曲线,下列判断中正确的是( )| A. | a代表的电阻丝较粗 | |
| B. | b代表的电阻丝较粗 | |
| C. | a、b电阻并联之后的总电阻的伏安特性曲线应该落在 I 区域 | |
| D. | 图线表示的电阻丝的阻值与电压成正比 |
| A. | 物体的加速度为1m/s2 | |
| B. | 物体的加速度为4m/s2 | |
| C. | 第2s内物体的位移为14m | |
| D. | 物体的速度随时间变化的关系式为v=3+2t |
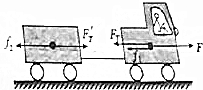 如图所示,一辆汽车拉着一辆拖车在平直道路上行驶,汽车的牵引力是F=16170N.汽车与拖车的质量分别是m1=5000kg和m2=2500kg,所受的阻力分别是f1=980N和f2=490N,求它们的加速度和汽车与拖车之间的拉力.
如图所示,一辆汽车拉着一辆拖车在平直道路上行驶,汽车的牵引力是F=16170N.汽车与拖车的质量分别是m1=5000kg和m2=2500kg,所受的阻力分别是f1=980N和f2=490N,求它们的加速度和汽车与拖车之间的拉力.