题目内容
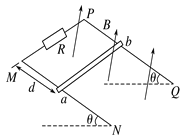
【题目】如图所示，平行金属导轨MN、PQ倾斜与水平面成30°角放置，其电阻不计，相距为l＝0.2 m。导轨顶端与电阻R相连，R＝1.5×10－2 Ω.在导轨上垂直导轨水平放置一根质量为m＝4×10－2 kg、电阻为r＝5×10－3 Ω的导体棒ab；ab距离导轨顶端d＝0.2 m，导体棒与导轨间的动摩擦因数
；在装置所在区域加一个垂直导轨平面，方向如图的磁场，磁感应强度B＝(0.2＋0.5t) T，g取10 m/s2。
(1)若导体棒被固定在导轨上，求通过电阻的电流；
(2)在哪一段时间内释放导体棒，导体棒将处于既不向下运动又不向上运动的静止状态？
(3)若t＝0时刻磁感应强度B0＝0.2 T，此时释放ab棒，要保证其以a＝2.5 m/s2的加速度沿导轨向下做初速度为零的匀加速直线运动，求磁感应强度B应该如何随时间变化，写出其表达式。
【答案】(1) 1 A(2) 平衡状态(3) 
【解析】试题分析：根据法拉第电磁感应定律和闭合电路欧姆定律求解电流强度；对导体棒根据平衡条件列方程，由于导体棒处于平衡状态满足-μmgcosθ≤f≤μmgcosθ，联立求解时间范围；对导体棒，根据牛顿第二定律列方程得到安培力为零，则回路中磁通量保持不变，根据磁通量相等列方程求解B随时间变化关系。
设闭合回路产生的感应电动势为E，有
磁通量变化率为： 
感应电流为： 
(2)若导体棒即将向下运动，则
安培力为：F1＝B1Il，
摩擦力为：Ff1＝μmgcos θ
由平衡条件得：F1＋Ff1＝mgsin θ
解得：t1＝0.6 s
若导体棒即将向上运动，则
安培力为：F2＝B2Il
摩擦力为：Ff2＝μmgcos θ
由平衡条件得：F2－Ff2＝mgsin θ
得：t2＝2.6 s
故在t＝0.6～2.6 s时间段内释放导体棒时，导体棒处于平衡状态
(3)对导体棒，由牛顿第二定律得：mgsin θ－μmgcos θ－BIl＝ma
故BIl＝0，即回路中感应电流为零.若要保证回路中感应电流为零，
则必须回路中磁通量保持不变.
则t时刻磁通量
解得： 
