题目内容
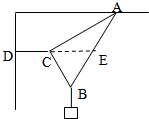 如图所示,物体重G=300N,绳CD恰呈水平状态,∠CAB=30°,∠ACB=90°,E是AB中点,CE也呈水平状态,那么AB段、CD段绳的张力分别为多少?
如图所示,物体重G=300N,绳CD恰呈水平状态,∠CAB=30°,∠ACB=90°,E是AB中点,CE也呈水平状态,那么AB段、CD段绳的张力分别为多少?分析:对结点B分析,由共点力的平衡条件可求得AB的拉力,再对结点C受力分析,由共点力平衡可求得CD的拉力.
解答: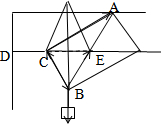 解:对B受力分析,可知B点受AB、BC及重物的拉力,而BC与AB的合力与重力大小相等方向相反,由图可知:
解:对B受力分析,可知B点受AB、BC及重物的拉力,而BC与AB的合力与重力大小相等方向相反,由图可知:
由几何关系可知:
TCB=TAB …①
2TABcos30°=G …②
∴TAB=100
N …③
对C点分析,C点受CD、BC及AC的拉力而处于平衡; 故AC的拉力与BC的拉力的合力与DC的拉力大小相等,方向相反;
由几何关系可知:
TCD=
…④
∴TCD=200
N
答:AB的拉力为100
N,CD段的拉力为200
N.
 解:对B受力分析,可知B点受AB、BC及重物的拉力,而BC与AB的合力与重力大小相等方向相反,由图可知:
解:对B受力分析,可知B点受AB、BC及重物的拉力,而BC与AB的合力与重力大小相等方向相反,由图可知:由几何关系可知:
TCB=TAB …①
2TABcos30°=G …②
∴TAB=100
| 3 |
对C点分析,C点受CD、BC及AC的拉力而处于平衡; 故AC的拉力与BC的拉力的合力与DC的拉力大小相等,方向相反;
由几何关系可知:
TCD=
| TCB |
| sin30° |
∴TCD=200
| 3 |
答:AB的拉力为100
| 3 |
| 3 |
点评:解决共点力的平衡题目,受力分析是关键,通过受力分析可以将抽象的力转化为形象的几何图形,由几何关系可得出待求力,在解题中要注意熟练解题的步骤和方法.

练习册系列答案
相关题目
 如图所示,物体重G=100N,保持静止.绳AC与BC分别与竖直方向成30°角和60°角,则绳AC的拉力为
如图所示,物体重G=100N,保持静止.绳AC与BC分别与竖直方向成30°角和60°角,则绳AC的拉力为 如图所示,物体重G=100N,并保持静止.绳子AC与BC分别与竖直方向成30°角和60°角,则绳子AC和BC的拉力分别为多大?
如图所示,物体重G=100N,并保持静止.绳子AC与BC分别与竖直方向成30°角和60°角,则绳子AC和BC的拉力分别为多大?