题目内容
8.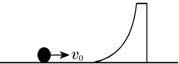 如图所示,质量为km的斜劈,其中k>1,静止放在光滑的水平面上,斜劈的曲面光滑且为半径为R的四分之一圆面,圆面下端与光滑水平面相切.一质量为m的小球位于水平面上某位置,现给小球水平向右的初速度v0.
如图所示,质量为km的斜劈,其中k>1,静止放在光滑的水平面上,斜劈的曲面光滑且为半径为R的四分之一圆面,圆面下端与光滑水平面相切.一质量为m的小球位于水平面上某位置,现给小球水平向右的初速度v0.①若R足够大,求当小球从斜劈滑下离开时小球的速度v1;
②若小球向右滑上斜劈刚好没有越过圆面上端,求k的取值.
分析 ①系统动量守恒,由动量守恒定律与机械能守恒定律求出速度.
②由动量守恒定律求出速度,然后根据题意确定k的值.
解答 解:①设小球从斜劈滑下离开时,小球和斜劈的速度分别为v1和v2,
系统动量守恒,以向右为正方向,由动量守恒可得:mv0=-mv1+kmv2,
由机械能守恒可得:$\frac{1}{2}$mv02=$\frac{1}{2}$mv12+$\frac{1}{2}$kmv22,
联立解得,小球速度为:v1=$\frac{1-k}{1+k}$v0;
②小球向右滑上斜劈刚好没有越过圆面上端,
说明两者在圆面最上端具有相同的速度v3,
系统在水平方向动量守恒,由动量守恒可得:mv0=(m+km)v3,
由机械能守恒可得:$\frac{1}{2}$mv02=$\frac{1}{2}$(m+km)v32+mgR,解得:k=$\frac{2gR}{{v}_{0}^{2}-2gR}$;
答:①若R足够大,求当小球从斜劈滑下离开时小球的速度v1为$\frac{1-k}{1+k}$v0;
②若小球向右滑上斜劈刚好没有越过圆面上端,k的取值为$\frac{2gR}{{v}_{0}^{2}-2gR}$.
点评 本题考查了动量守恒定律的应用,分析清楚物体运动过程,应用动量守恒定律与机械能守恒定律即可正确解题.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
18.功率为10W的发光二极管(LED灯)的亮度与功率60W的白炽灯相当.假设每户家庭有二只60W的白炽灯,均用10W的LED灯替代,试估算人口约450万的嘉兴一天可节约的电能最接近( )
| A. | 9×105kW•h | B. | 9×106kW•h | C. | 9×107kW•h | D. | 9×108kW•h |
19.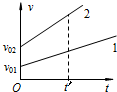 在如图所示的速度图象中,图线1、2分别表示质点B运动速度和时间的函数关系,v01、v02表示A、B质点各自运动的初速度,a1、a2表示A、B质点运动的加速度,根据图象可知:( )
在如图所示的速度图象中,图线1、2分别表示质点B运动速度和时间的函数关系,v01、v02表示A、B质点各自运动的初速度,a1、a2表示A、B质点运动的加速度,根据图象可知:( )
 在如图所示的速度图象中,图线1、2分别表示质点B运动速度和时间的函数关系,v01、v02表示A、B质点各自运动的初速度,a1、a2表示A、B质点运动的加速度,根据图象可知:( )
在如图所示的速度图象中,图线1、2分别表示质点B运动速度和时间的函数关系,v01、v02表示A、B质点各自运动的初速度,a1、a2表示A、B质点运动的加速度,根据图象可知:( )| A. | v01>v02 a1>a2 | B. | v01<v02 a1>a2 | C. | v01>v02 a1<a2 | D. | v01<v02 a1<a2 |
16.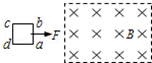 如图所示,金属线框abcd置于光滑水平桌面上,其右方存在一个有理想边界的方向竖直向下的矩形匀强磁场区,磁场宽度大于线圈宽度.金属线框在水平恒力F作用下向右运动,ab边始终保持与磁场边界平行.ab边进入磁场时线框恰好能做匀速运动.则下列说法中正确的是( )
如图所示,金属线框abcd置于光滑水平桌面上,其右方存在一个有理想边界的方向竖直向下的矩形匀强磁场区,磁场宽度大于线圈宽度.金属线框在水平恒力F作用下向右运动,ab边始终保持与磁场边界平行.ab边进入磁场时线框恰好能做匀速运动.则下列说法中正确的是( )
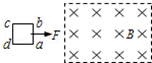 如图所示,金属线框abcd置于光滑水平桌面上,其右方存在一个有理想边界的方向竖直向下的矩形匀强磁场区,磁场宽度大于线圈宽度.金属线框在水平恒力F作用下向右运动,ab边始终保持与磁场边界平行.ab边进入磁场时线框恰好能做匀速运动.则下列说法中正确的是( )
如图所示,金属线框abcd置于光滑水平桌面上,其右方存在一个有理想边界的方向竖直向下的矩形匀强磁场区,磁场宽度大于线圈宽度.金属线框在水平恒力F作用下向右运动,ab边始终保持与磁场边界平行.ab边进入磁场时线框恰好能做匀速运动.则下列说法中正确的是( )| A. | 线框穿出磁场过程中,一定先做减速运动 | |
| B. | 线框完全处于磁场中的运动阶段,F做的功大于线框动能的增加量 | |
| C. | 线框进入磁场过程,F做的功大于线框内增加的内能 | |
| D. | 线框穿出磁场过程中,F做的功等于线框中产生的焦耳热 |
13.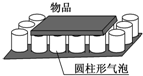 一种减震垫如图所示,上面布满了圆柱状薄膜气泡,每个气泡内充满气体,当平板状物品平放在气泡上时,气泡被挤压.气泡内气体可视为理想气体,假设袋内气体与外界无热交换,则袋内气体( )
一种减震垫如图所示,上面布满了圆柱状薄膜气泡,每个气泡内充满气体,当平板状物品平放在气泡上时,气泡被挤压.气泡内气体可视为理想气体,假设袋内气体与外界无热交换,则袋内气体( )
 一种减震垫如图所示,上面布满了圆柱状薄膜气泡,每个气泡内充满气体,当平板状物品平放在气泡上时,气泡被挤压.气泡内气体可视为理想气体,假设袋内气体与外界无热交换,则袋内气体( )
一种减震垫如图所示,上面布满了圆柱状薄膜气泡,每个气泡内充满气体,当平板状物品平放在气泡上时,气泡被挤压.气泡内气体可视为理想气体,假设袋内气体与外界无热交换,则袋内气体( )| A. | 体积减小,内能增大 | B. | 体积减小,压强减小 | ||
| C. | 对外界做负功,内能增大 | D. | 对外界做正功,压强减小 |
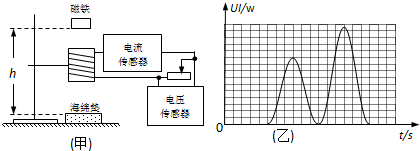
20.如下图(甲)所示,打开电流和电压传感器,将磁铁置于螺线管正上方距海绵垫高为h处静止释放,磁铁穿过螺线管后掉落到海绵垫上并静止.若磁铁下落过程中受到的磁阻力远小于磁铁重力,且不发生转动,不计线圈电阻.图(乙)是计算机荧屏上显示的UI-t曲线,其中的两个峰值是磁铁刚进入螺线管内部和刚从内部出来时产生的.下列说法正确的是( )

| A. | 若仅增大h,两个峰值间的时间间隔会增大 | |
| B. | 若仅减小h,两个峰值都会减小 | |
| C. | 若仅减小h,两个峰值可能会相等 | |
| D. | 若仅增大滑动变阻器的阻值,两个峰值都会增大 |
18.有一电流计,内阻Rg=25Ω,满偏电流Ig=3mA,现对它进行改装,下列说法正确的是( )
| A. | 把它改装成量程为0.6A的电流表,需与它并联一个0.126Ω的电阻 | |
| B. | 把它改装成量程为0.6A的电流表,需与它串联一个0.126Ω的电阻 | |
| C. | 把它改装成量程为3v的电压表,需与它并联一个975Ω的电阻 | |
| D. | 把它改装成量程为3v的电压表,需与它串联一个975Ω的电阻 |
 LED绿色照明技术已经走进我们的生活.某实验小组要精确测定额定电压为3V的LED灯正常工作时的电阻,已知该灯正常工作时电阻大约500Ω,电学符号与小灯泡电学符号相同.
LED绿色照明技术已经走进我们的生活.某实验小组要精确测定额定电压为3V的LED灯正常工作时的电阻,已知该灯正常工作时电阻大约500Ω,电学符号与小灯泡电学符号相同.
