题目内容
18.质量m=2.0×10-4kg、电荷量q=1.0×10-6C的带正电微粒静止在空间范围足够大的匀强电场中,电场强度大小为E1.在t=0时刻,电场强度突然增加到E2=4.0×103N/C,到t=0.20s时再把电场方向改为水平向右,场强大小保持不变,取g=10m/s2.求:(1)t=0.20s时间内带电微粒上升的高度;
(2)电场方向改为水平向右后带电微粒最小的动能.
分析 (1)由牛顿第二定律求出微粒的加速度,然后由匀变速直线运动的位移公式求出位移.
(2)求出微粒动能的表达式,然后求出微粒的最小动能.
解答 解:(1)在电场E2中微粒向上做初速度为零的匀加速直线运动,
由牛顿第二定律得:qE2-mg=ma1,
代入数据解得:a1=10m/s2,
t=0.2s末微粒上升的高度:h=$\frac{1}{2}$a1t2=$\frac{1}{2}$×10×0.22=0.2m;
(2)t=0.2s时微粒的速度:v1=a1t=2m/s,
电场方向变为水平后,微粒在水平方向做初速度为零的匀加速直线运动,竖直方向做匀减速直线运动,
经时间t1微粒动能最小,水平方向的加速度:a2=$\frac{q{E}_{2}}{m}$=20m/s2,
竖直方向的速度:vy=v1-gt1=2-10t1,
水平方向的速度:vx=a2t1=20t1,
微粒的动能:EK=$\frac{1}{2}$m(vx2+vy2)=$\frac{1}{2}$m[(a2t1)2+(v1-gt1)2]=$\frac{1}{2}$m[(a22+g2)t12-2v1gt1+v12],
当t1=$\frac{{v}_{1}g}{{a}_{2}^{2}+{g}^{2}}$=0.04s时,微粒的动能最小,动能最小值为:EK最小=3.2×10-4J;
答:(1)t=0.20s时间内带电微粒上升的高度为0.2m;
(2)电场方向改为水平向右后带电微粒最小的动能3.2×10-4J.
点评 本题考查了求微粒的位移、微粒的最小动能问题,分析清楚微粒运动过程、应用运动的合成与分解是正确解题的关键,应用牛顿第二定律、运动学公式与动能的计算公式可以解题,解题时注意数学最小的应用.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
13.电容器是一种常用的电子元件.对电容器认识正确的是( )
| A. | 电容器的电容表示其储存电荷能力 | |
| B. | 电容器的电容与它所带的电量成正比 | |
| C. | 电容器放电时电场能转化为其他形式的能 | |
| D. | 电容的常用单位有μF和pF,1μF=103pF |
3.关于磁感应强度,下面哪个说法正确( )
| A. | 磁感应强度的方向,就是通电直导线在磁场中的受力方向 | |
| B. | 磁感应强度大的地方通电导线在那里所受的力也一定大 | |
| C. | 磁感应强度的单位可以用Wb/m2表示 | |
| D. | 磁感应强度是标量 |
10. 2009年当地时间9月23日,在印度的萨蒂什•达万航天中心,一枚PSLV-C14型极地卫星运载火箭携带七颗卫星发射升空,成功实现“一箭七星”发射,相关图片如图所示.则下列说法正确的是( )
2009年当地时间9月23日,在印度的萨蒂什•达万航天中心,一枚PSLV-C14型极地卫星运载火箭携带七颗卫星发射升空,成功实现“一箭七星”发射,相关图片如图所示.则下列说法正确的是( )
 2009年当地时间9月23日,在印度的萨蒂什•达万航天中心,一枚PSLV-C14型极地卫星运载火箭携带七颗卫星发射升空,成功实现“一箭七星”发射,相关图片如图所示.则下列说法正确的是( )
2009年当地时间9月23日,在印度的萨蒂什•达万航天中心,一枚PSLV-C14型极地卫星运载火箭携带七颗卫星发射升空,成功实现“一箭七星”发射,相关图片如图所示.则下列说法正确的是( )| A. | 火箭发射时,喷出的高速气流对火箭的作用力大于火箭对气流的作用力 | |
| B. | 发射初期,火箭处于超重状态 | |
| C. | 高温高压燃气从火箭尾部喷出时对火箭的作用力与火箭对燃气的作用力是一对平衡力 | |
| D. | 发射的七颗卫星进入轨道正常运转后,均处于完全失重状态 |
7.做匀速圆周运动的二物体甲和乙,它们的向心加速度分别为a1和a2,且a1>a2,下列说法正确的是( )
| A. | 甲的速度方向比乙的速度方向变化得快 | |
| B. | 甲的角速度比乙的角速度小 | |
| C. | 甲的轨道半径比乙的轨道半径小 | |
| D. | 甲的线速度大于乙的线速度 |
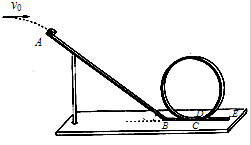 为了研究过山车的原理,物理兴趣小组提出了下列设想:如图所示,取一个与水平方向夹角为30°,长L=0.8m的倾斜轨道AB,通过水平轨道BC与竖直圆轨道相连,出口为水平轨道DE,整个轨道都是光滑的,其中AB与BC轨道以微小圆弧相接,竖直圆轨道的半径R=0.6m,现使一个质量m=0.1kg的小物块从A点开始以初速度v0沿倾斜轨道滑下,g取10m/s2,问:
为了研究过山车的原理,物理兴趣小组提出了下列设想:如图所示,取一个与水平方向夹角为30°,长L=0.8m的倾斜轨道AB,通过水平轨道BC与竖直圆轨道相连,出口为水平轨道DE,整个轨道都是光滑的,其中AB与BC轨道以微小圆弧相接,竖直圆轨道的半径R=0.6m,现使一个质量m=0.1kg的小物块从A点开始以初速度v0沿倾斜轨道滑下,g取10m/s2,问: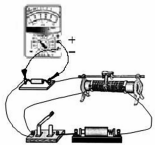 某同学用多用电表测量某定值电阻的阻值.
某同学用多用电表测量某定值电阻的阻值. 如图所示,坐标平面的第Ⅰ象限内存在方向水平向左的匀强电场,第Ⅳ象限内有两个极板M、N、质荷比为$\frac{m}{q}$=4×10-20kg/C的带正电粒子,在M极板表面处经M、N间加速电场加速后,从x轴上的A点以初速度v0=2×107m/s垂直x轴射入电场,OA=0.2m,之后粒子以与y轴正方向成60°角进入第Ⅱ象限,为了使该粒子能从C点垂直于x轴进入第Ⅲ象限,可在适当的地方加一个垂直于xOy平面、磁感应强度大小为B=0.16T的匀强磁场,若此磁场仅分布在一个圆形区域内.粒子重力不计.求:
如图所示,坐标平面的第Ⅰ象限内存在方向水平向左的匀强电场,第Ⅳ象限内有两个极板M、N、质荷比为$\frac{m}{q}$=4×10-20kg/C的带正电粒子,在M极板表面处经M、N间加速电场加速后,从x轴上的A点以初速度v0=2×107m/s垂直x轴射入电场,OA=0.2m,之后粒子以与y轴正方向成60°角进入第Ⅱ象限,为了使该粒子能从C点垂直于x轴进入第Ⅲ象限,可在适当的地方加一个垂直于xOy平面、磁感应强度大小为B=0.16T的匀强磁场,若此磁场仅分布在一个圆形区域内.粒子重力不计.求: