题目内容
 (2003?上海)质量为m的飞机以水平速度v0飞离跑道后逐渐上升,若飞机在此过程中水平速度保持不变,同时受到重力和竖直向上的恒定升力(该升力由其它力的合力提供,不含重力).今测得当飞机在水平方向的位移为l时,它的上升高度为h,求:
(2003?上海)质量为m的飞机以水平速度v0飞离跑道后逐渐上升,若飞机在此过程中水平速度保持不变,同时受到重力和竖直向上的恒定升力(该升力由其它力的合力提供,不含重力).今测得当飞机在水平方向的位移为l时,它的上升高度为h,求:(1)飞机受到的升力大小;
(2)从起飞到上升至h高度的过程中升力所作的功及在高度h处飞机的动能.
分析:(1)本题要将飞机的运动沿着水平和竖直方向正交分解,其水平分运动为匀速直线运动,竖直方向由于升力和重力都是恒力,合力恒定,加速度恒定,因而竖直方向为匀加速直线运动,可以先根据运动学公式求出加速度,然后根据牛顿第二定律列式求解;
(2)直接根据恒力做功的公式求出升力的功,可以根据分速度合成出合速度,然后根据动能的表达式求出动能.
(2)直接根据恒力做功的公式求出升力的功,可以根据分速度合成出合速度,然后根据动能的表达式求出动能.
解答:解:(1)飞机水平方向分运动的分速度不变,是匀速运动,故
l=v0t ①
y方向分运动加速度恒定,是匀加速运动,故
h=
at2 ②
由①②两式消去t,即得
a=
③
由牛顿第二定律
F-mg=ma ④
由③④两式解得
F=mg+ma=mg(1+
)
即飞机受到的升力大小为mg(1+
).
(2)由恒力做功的表达式,可知升力做功
W=Fh=mgh(1+
)
在h处,竖直分速度为
vt=at=
=
合速度为
v=
因而动能为
Ek=
m(
+
)=
m
(1+
)
即从起飞到上升至h高度的过程中升力所作的功为mgh(1+
),在高度h处飞机的动能为
m
(1+
).
l=v0t ①
y方向分运动加速度恒定,是匀加速运动,故
h=
| 1 |
| 2 |
由①②两式消去t,即得
a=
| 2h |
| l2 |
| v | 2 0 |
由牛顿第二定律
F-mg=ma ④
由③④两式解得
F=mg+ma=mg(1+
| 2h |
| gl2 |
| v | 2 0 |
即飞机受到的升力大小为mg(1+
| 2h |
| gl2 |
| v | 2 0 |
(2)由恒力做功的表达式,可知升力做功
W=Fh=mgh(1+
| 2h |
| gl2 |
| v | 2 0 |
在h处,竖直分速度为
vt=at=
| 2ah |
| 2hv0 |
| l |
合速度为
v=
|
因而动能为
Ek=
| 1 |
| 2 |
| v | 2 0 |
| v | 2 t |
| 1 |
| 2 |
| v | 2 0 |
| 4h2 |
| l2 |
即从起飞到上升至h高度的过程中升力所作的功为mgh(1+
| 2h |
| gl2 |
| v | 2 0 |
| 1 |
| 2 |
| v | 2 0 |
| 4h2 |
| l2 |
点评:本题关键将飞机的运动分解为水平方向的匀速直线运动和竖直方向的匀加速直线运动,再根据运动学公式和牛顿第二定律列式后联立求解.

练习册系列答案
相关题目
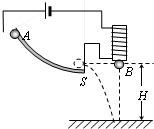 (2003?上海)如图所示,在研究平抛运动时,小球A沿轨道滑下,离开轨道末端(末端水平)时撞开轻质接触式开关S,被电磁铁吸住的小球B同时自由下落.改变整个装置的高度H做同样的实验,发现位于同一高度的A、B两球总是同时落地,该实验现象说明了A球在离开轨道后
(2003?上海)如图所示,在研究平抛运动时,小球A沿轨道滑下,离开轨道末端(末端水平)时撞开轻质接触式开关S,被电磁铁吸住的小球B同时自由下落.改变整个装置的高度H做同样的实验,发现位于同一高度的A、B两球总是同时落地,该实验现象说明了A球在离开轨道后