题目内容
5. 一辆长途客车正以v0=20m/s的速度匀速行驶,突然,司机看见车的正前方x=33m处有一只狗,如图所示.司机经过t0=0.5s的反应时间后,采取制动措施,再经t1=4s的制动时间后客车停止.
一辆长途客车正以v0=20m/s的速度匀速行驶,突然,司机看见车的正前方x=33m处有一只狗,如图所示.司机经过t0=0.5s的反应时间后,采取制动措施,再经t1=4s的制动时间后客车停止.(1)求长途客车制动时的加速度;
(2)求长途客车司机从发现狗至客车停止运动的这段时间内前进的距离;
(3)若狗以v=4m/s的速度与长途客车同向匀速奔跑,试通过计算说明狗会不会被撞?
分析 (1)根据匀变速直线运动的速度时间公式求出制动时的加速度.
(2)反应时间内客车做匀速直线运动,刹车后做匀减速运动,结合匀速运动的位移和匀减速运动的位移求出这段时间内前进的距离.
(3)根据速度时间公式求出两者速度相等的时间,结合位移关系判断两者是否相撞.
解答 解:(1)客车制动时的加速度a=$\frac{0-{v}_{0}}{{t}_{1}}=\frac{-20}{4}m/{s}^{2}=-5m/{s}^{2}$.
(2)反应时间内客车的位移x1=v0t0=20×0.5m=10m,
刹车后的位移${x}_{2}=\frac{{v}_{0}}{2}{t}_{1}=\frac{20}{2}×4m=40m$,
则x=x1+x2=10+40m=50m.
(3)客车和狗速度相等经历的时间$t′=\frac{v-{v}_{0}}{a}=\frac{4-20}{-5}s=3.2s$,
客车刹车的位移${x}_{2}′=\frac{{v}^{2}-{{v}_{0}}^{2}}{2a}=\frac{16-400}{-10}m=38.4m$,
狗的位移x3=v(t0+t′)=4×(3.2+0.5)m=14.8m,
因为x3+x<x1+x2′,则狗会被撞上.
答:(1)长途客车制动时的加速度为-5m/s2;
(2)长途客车司机从发现狗至客车停止运动的这段时间内前进的距离为50m.
(3)狗会被撞上.
点评 解决本题的关键知道客车在整个过程中的运动规律,结合运动学公式灵活求解,对于第三问,考查运动学中的追及问题,抓住速度时的位移分析判断.

练习册系列答案
相关题目
15.关于加速、减速直线运动,下列说法中正确的是( )
| A. | 加速度大小在逐渐减小,速度一定在逐渐减小 | |
| B. | 加速度大小在逐渐减小,速度可能在逐渐增大 | |
| C. | 只要加速度和速度方向相同,物体的速度就一定增大 | |
| D. | 加速度和速度方向相反,物体的速度可能在减小 |
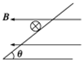
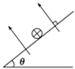
20. 如图所示,仅在电场力作用下,一带负电粒子沿图中虚线从A运动到B,则( )
如图所示,仅在电场力作用下,一带负电粒子沿图中虚线从A运动到B,则( )
 如图所示,仅在电场力作用下,一带负电粒子沿图中虚线从A运动到B,则( )
如图所示,仅在电场力作用下,一带负电粒子沿图中虚线从A运动到B,则( )| A. | 电场力对粒子做正功 | B. | 粒子电势能减少 | ||
| C. | 粒子动能减少 | D. | 粒子加速度不变 |
10.关于自由落体运动的加速度g,下列说法中正确的是( )
| A. | 重力加速度g是标量,只有大小没有方向,通常计算中g=9.8m/s2 | |
| B. | 同一地点、轻和重的物体的g值一样大 | |
| C. | g值在地球上任何地方都一样大 | |
| D. | 随纬度越高,g值越小 |
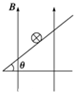
17.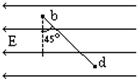 如图所示,一带电液滴在重力和匀强电场对它的作用力作用下,从静止开始由b沿直线运动到d,且bd与竖直方向所夹的锐角为45°,则下列结论错误的是( )
如图所示,一带电液滴在重力和匀强电场对它的作用力作用下,从静止开始由b沿直线运动到d,且bd与竖直方向所夹的锐角为45°,则下列结论错误的是( )
 如图所示,一带电液滴在重力和匀强电场对它的作用力作用下,从静止开始由b沿直线运动到d,且bd与竖直方向所夹的锐角为45°,则下列结论错误的是( )
如图所示,一带电液滴在重力和匀强电场对它的作用力作用下,从静止开始由b沿直线运动到d,且bd与竖直方向所夹的锐角为45°,则下列结论错误的是( )| A. | 此液滴带正电 | B. | 液滴做匀加速直线运动 | ||
| C. | 合外力对液滴做的总功等于零 | D. | 液滴的电势能减少 |
11.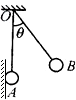 如图,A、B两个带电小球用等长绝缘细线悬挂于O点,A球固定,B球受到库仑力作用与细线间成一定的夹角,若其中一个小球由于漏电,电荷量缓慢减小,则关于A、B两球的间距和库仑力大小的变化,下列说法中正确的是( )
如图,A、B两个带电小球用等长绝缘细线悬挂于O点,A球固定,B球受到库仑力作用与细线间成一定的夹角,若其中一个小球由于漏电,电荷量缓慢减小,则关于A、B两球的间距和库仑力大小的变化,下列说法中正确的是( )
 如图,A、B两个带电小球用等长绝缘细线悬挂于O点,A球固定,B球受到库仑力作用与细线间成一定的夹角,若其中一个小球由于漏电,电荷量缓慢减小,则关于A、B两球的间距和库仑力大小的变化,下列说法中正确的是( )
如图,A、B两个带电小球用等长绝缘细线悬挂于O点,A球固定,B球受到库仑力作用与细线间成一定的夹角,若其中一个小球由于漏电,电荷量缓慢减小,则关于A、B两球的间距和库仑力大小的变化,下列说法中正确的是( )| A. | 间距变小,库仑力变大 | B. | 间距变小,库仑力变小 | ||
| C. | 间距变小,绳子拉力不变 | D. | 间距不变,库仑力减小 |
12. 质量为m的小球被长为L的细绳拉着由A点(O、A两点在同一水平面上)静止释放,经过一段时间到达最低点B,在B点速度大小为v,则以下说法正确的是( )
质量为m的小球被长为L的细绳拉着由A点(O、A两点在同一水平面上)静止释放,经过一段时间到达最低点B,在B点速度大小为v,则以下说法正确的是( )
 质量为m的小球被长为L的细绳拉着由A点(O、A两点在同一水平面上)静止释放,经过一段时间到达最低点B,在B点速度大小为v,则以下说法正确的是( )
质量为m的小球被长为L的细绳拉着由A点(O、A两点在同一水平面上)静止释放,经过一段时间到达最低点B,在B点速度大小为v,则以下说法正确的是( )| A. | 小球在B点时重力的瞬时功率为mgv | |
| B. | 绳子的拉力不做功 | |
| C. | 由A到B过程,小球重力的瞬时功率先增大后减小 | |
| D. | 小球在B点时的重力势能为0 |