题目内容
11.利用图(a)所示实验装置可粗略测量人吹气产生的压强.两端开口的细玻璃管水平放置,管内塞一潮湿小棉球,实验者从玻璃管的一端A吹气,棉球从另一端B飞出,测得玻璃管内部截面积S,距地面高度h,棉球质量m,开始时棉球的静止位置与管口B的距离x,落地点C与管口B的水平距离l,然后多次改变x,测出对应的l,画出l2-x关系图线如图(b)所示,并由此得出相应的斜率k.
(1)若不计棉球在空中运动时的空气阻力,根据以上测得的物理量可得,棉球从B端飞出时速度v0=$l\sqrt{\frac{g}{2h}}$.
(2)假设实验者吹气能保持玻璃管内气体压强始终为恒定值,不计棉球与管壁的摩擦,重力加速度g、大气压强p0均为已知,利用图(b)中直线的斜率k可得,管内气体压强p=p0+$\frac{kmg}{4Sh}$.
(3)考虑到实验时棉球与管壁间有摩擦力,则(2)中得到的p与实际压强相比偏小(填“偏大”、“偏小”).
分析 (1)棉球从B端飞出做平抛运动,可以根据平抛运动的基本公式解出速度v0;
(2)根据压强公式求出压力F,运用动能定理求出l2-x的关系,其斜率等于k,这样就可以求出管内气体压强p;
(3)考虑到实验时棉球与管壁间有摩擦,所以除了压力做功外,摩擦力对棉球做负功,再运用动能定理求出l2-x的关系,其斜率等于k,这样就可以比较压强偏大还是偏小.
解答 解:(1)棉球从B端飞出做平抛运动,根据平抛运动的基本公式得:
l=v0t,h=$\frac{1}{2}g{t}^{2}$
解得:v0=l$\sqrt{\frac{g}{2h}}$
(2)设玻璃管内气体压强始终为p,不计棉球与管壁的摩擦,对棉球从静止到B点的运动过程运用动能定理得:
(p-p0)Sx=$\frac{1}{2}m{{v}_{0}}^{2}$
(p-p0)Sx=$\frac{1}{2}m{(l\sqrt{\frac{g}{2h}})}^{2}$
所以l2=$\frac{4(p-{p}_{0})\;Sh}{mg}x$=kx
所以$\frac{4(p-{p}_{0})\;Sh}{mg}=\;k$
解得:p=p0+$\frac{kmg}{4Sh}$
(3)考虑到实验时棉球与管壁间有摩擦,设摩擦力为f,所以除了压力做功外,摩擦力对棉球做负功,再运用动能定理得:
(p实-p0)Sx-fx=$\frac{1}{2}m{{v}_{0}}^{2}$
l2=$\frac{4h[({p}_{实}-{p}_{0})S-f]}{mg}x$=kx
所以$\frac{4h[({p}_{实}-{p}_{0})S-f]}{mg}=k$
解得:p实=p0+$\frac{kmg+4fh}{4Sh}$
很明显,(2)中得到的p与实际压强相比偏小.
故答案为:(1)l$\sqrt{\frac{g}{2h}}$;(2)p0+$\frac{kmg}{4Sh}$;(3)偏小.
点评 该题考查了平抛运动的基本规律与压强的相关计算,要求同学们学会熟练运用动能定理解题,比较简洁、方便,本题难度不大.

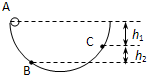 如图所示,一物体从圆弧形轨道的A点无初速滑下,物体与圆弧轨道间的动摩擦因数为μ,由于摩擦力的作用物体沿轨道到达C点时的速度为零,C点比A点下降了h1,物体又由C点沿轨道滑至B点,速度再次为零,B比C下降了h2,则h1与h2比较有( )
如图所示,一物体从圆弧形轨道的A点无初速滑下,物体与圆弧轨道间的动摩擦因数为μ,由于摩擦力的作用物体沿轨道到达C点时的速度为零,C点比A点下降了h1,物体又由C点沿轨道滑至B点,速度再次为零,B比C下降了h2,则h1与h2比较有( )| A. | h1>h2 | B. | h1<h2 | C. | h1=h2 | D. | 无法确定 |
| A. | 力和位移都是矢量,所以功也是矢量 | |
| B. | 正功大于负功 | |
| C. | 人能够搬动重物做功,说明人具有能量 | |
| D. | 机械效率高,表示机械做功快 |
| A. | 只将角速度ω增大1倍 | B. | 只将线圈边长L增大至2L | ||
| C. | 只将线圈匝数增加至2n | D. | 只将磁感应强度增至2B |
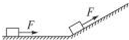 如图所示,大小不变的力F拉着物体先在光滑的水平面上运动位移s,F做功为W1;接着沿一粗糙斜面向上拉动物体,又运动了位移s,F做功为W2,以下说法正确的是( )
如图所示,大小不变的力F拉着物体先在光滑的水平面上运动位移s,F做功为W1;接着沿一粗糙斜面向上拉动物体,又运动了位移s,F做功为W2,以下说法正确的是( )| A. | W1>W2 | B. | W1<W2 | ||
| C. | W1=W2 | D. | 以上三种情况都有可能 |
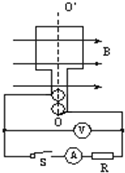 如图所示为交流发电机示意图,匝数为n=100匝的矩形线圈,边长分别为10cm和20cm,内阻为5Ω,在磁感应强度B=0.5T的匀强磁场中绕OO′轴以50$\sqrt{2}$rad/s的角速度匀速转动,转动开始时线圈平面与磁场方向平行,线圈通过电刷和外部20Ω的电阻R相接.求电键S合上后,
如图所示为交流发电机示意图,匝数为n=100匝的矩形线圈,边长分别为10cm和20cm,内阻为5Ω,在磁感应强度B=0.5T的匀强磁场中绕OO′轴以50$\sqrt{2}$rad/s的角速度匀速转动,转动开始时线圈平面与磁场方向平行,线圈通过电刷和外部20Ω的电阻R相接.求电键S合上后, 如图1所示,有一秒摆(周期为2s的单摆),悬点为O,在O点正下方M处有一钉子,从平衡位置向左摆时由于钉子的阻碍改变了摆的长度,从平衡位置向右摆时又变为原摆的长度,其振动图象如图2所示.g取9.86m/s2,求:
如图1所示,有一秒摆(周期为2s的单摆),悬点为O,在O点正下方M处有一钉子,从平衡位置向左摆时由于钉子的阻碍改变了摆的长度,从平衡位置向右摆时又变为原摆的长度,其振动图象如图2所示.g取9.86m/s2,求: 如图所示,固定的光滑半球形容器半径为R,其最底点C与球心O的连线垂直水平面,质量为m的小球在A点以某个初速沿着半球容器切线下滑,恰能滑到容器边沿B处.在这过程中重力做功为-0.6mgR;弹力做功为0;球在A处的速度大小为$\sqrt{1.2gR}$.
如图所示,固定的光滑半球形容器半径为R,其最底点C与球心O的连线垂直水平面,质量为m的小球在A点以某个初速沿着半球容器切线下滑,恰能滑到容器边沿B处.在这过程中重力做功为-0.6mgR;弹力做功为0;球在A处的速度大小为$\sqrt{1.2gR}$. 如图所示,杆长为L,杆的一端固定一质量为m的小球,杆的质量忽略不计,整个系统绕杆的另一端O在竖直平面内作圆周运动,求:
如图所示,杆长为L,杆的一端固定一质量为m的小球,杆的质量忽略不计,整个系统绕杆的另一端O在竖直平面内作圆周运动,求: