题目内容
1．质量为2.0kg的滑块，以4m/s的速度在光滑水平面上向右滑行．若从某一时刻起受到一个向左的恒力的作用，经过一段时间后速度变为6m/s，方向向左．在这段时间内，恒力对滑块做的功是（ ）| A． | 0 | B． | 8J | C． | 20J | D． | 32J |
分析 由题意可明确滑块的初末状态及外力做功情况；再由动能定理可以求出恒力对滑块所做的功．
解答 解：滑块运动过程中，只有恒力对其做功，则由动能定理可知：恒力做的功：W=$\frac{1}{2}$mv′2-$\frac{1}{2}$mv2=$\frac{1}{2}×2×（{6}^{2}-{4}^{2}）$J=20J
故选：C
点评 本题考查动能定理的应用，要注意正确选择初末状态并做好受力分析，明确哪些力做功；同时注意动能是标量，与速度方向无关．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
如图，额定电压为100V的灯泡由实验得到的I-U图线．若将规格为100Ω的定值电阻与灯泡串联后接在100V的电源上，则此时灯泡的实际功率为多少？
9．如果气球与所载物体的总质量为M，以加速度以a（a＜g）一向上加速升起，那么要使气球以大小相等的加速度向下降落，气球的载荷应增加$\frac{2Ma}{g-a}$才行．（气球浮力不变，空气阻力不计）
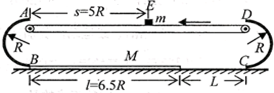如图所示，以A、B和C、D为断点的两半圆形光滑轨道固定于竖直平面内，一滑板静止在光滑的地面上，左端紧靠B点，上表面所在平面与两半圆分别相切于B、C两点，一物块（视为质点）被轻放在水平匀速运动的传送带上E点，运动到A点时刚好与传送带速度相同，然后经A点沿半圆轨道滑下，再经B点滑上滑板，滑板运动到C点时被牢固粘连．物块可视为质点，质量为m，滑板质量为M=2m，两半圆半径均为R，板长l=6.5R，板右端到C点的距离L在R＜L＜5R范围内取值，E点距A点的距离s=5R，物块与传送带、物块与滑板间的动摩擦因数均为μ=0.5，重力加速度g已知．
13．在做“研究平抛运动”实验中，以下那些操作可能引起实验误差（ ）
| A． | 安装斜槽时，斜槽末端切线方向不水平 | |
| B． | 确定OY轴时，没有用重垂线 | |
| C． | 斜槽不是绝对光滑的，有一定摩擦 | |
| D． | 每次从轨道同一位置释放小球 |
如图所示，氢核（11H）、氘核（21H）、氚核（31H）分别由左孔从静止释放．后由右孔射出，则：
11．以a=$\frac{g}{2}$的加速度加速下降的气球、吊篮和沙袋的总质量为M，欲使该气球以同样大小的加速度匀加速上升，则从吊篮中抛出的沙袋质量应是总质量的（ ）
| A． | $\frac{1}{2}$ | B． | $\frac{1}{4}$ | C． | $\frac{3}{4}$ | D． | $\frac{2}{3}$ |