题目内容
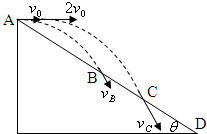 如图所示,从足够长的固定斜面的顶端A先、后两次水平抛出一小球,第一次抛出时的初速度为v0,第二次抛出时的初速度为2v0,小球落到斜面前瞬间,其速度大小分别vB、vC(注:vB、vc为未知).已知斜面的倾角为θ,重力加速度为g.不计空气阻力.
如图所示,从足够长的固定斜面的顶端A先、后两次水平抛出一小球,第一次抛出时的初速度为v0,第二次抛出时的初速度为2v0,小球落到斜面前瞬间,其速度大小分别vB、vC(注:vB、vc为未知).已知斜面的倾角为θ,重力加速度为g.不计空气阻力.(1)求小球从A到B的时间t1
(2)求小球自第二次抛出到离斜面最远点所用的时间t2
(3)试证明速度vB、vC的方向平行.
分析:(1)小球做的是平抛运动,根据水平和竖直方程的位移与斜面的夹角的关系,可以求得从A到B的时间t1;
(2)当速度v方向与斜面平行时,小球离斜面最远,根据此时的速度方程可以求得时间t2;
(3)第一次和第二次,小球都落在斜面上,根据平抛运动的水平速度和竖直速度,以及位移之间的关系,可以得出vB、vC的方向.
(2)当速度v方向与斜面平行时,小球离斜面最远,根据此时的速度方程可以求得时间t2;
(3)第一次和第二次,小球都落在斜面上,根据平抛运动的水平速度和竖直速度,以及位移之间的关系,可以得出vB、vC的方向.
解答: 解:(1)对位移AB分解,有
解:(1)对位移AB分解,有
水平分位移x1=v0t 竖直分位移y1=
gt2
由图可知tanθ=
=
解得 t1=
(2)当速度v方向与斜面平行时,小球离斜面最远,对此时速度v分解 有
水平分速度vx=2v0 竖直分速度 vy=gt2
由右图知:tanθ=
解得 t2=
(3)证明:设速度vB、vC与水平方向的夹角分别为α1、α2
对位移分解,由(1)问可知:tanθ=
=
对速度分解,由(2)问可知:tanα=
=
由上两式得 tanα=2tanθ
所以 tanα1=2tanθ=tanα2,
即证得 速度vB、vC与的方向平行
答:(1)小球从A到B的时间t1为
;
(2)小球自第二次抛出到离斜面最远点所用的时间t2为
;
(3)证明过程如上.
 解:(1)对位移AB分解,有
解:(1)对位移AB分解,有水平分位移x1=v0t 竖直分位移y1=
| 1 |
| 2 |
由图可知tanθ=
| y1 |
| x1 |
| gt1 |
| 2v0 |
解得 t1=
| 2v0tanθ |
| g |
(2)当速度v方向与斜面平行时,小球离斜面最远,对此时速度v分解 有
水平分速度vx=2v0 竖直分速度 vy=gt2
由右图知:tanθ=
| vy |
| vx |
解得 t2=
| 2v0tanθ |
| g |
(3)证明:设速度vB、vC与水平方向的夹角分别为α1、α2
对位移分解,由(1)问可知:tanθ=
| y |
| x |
| gt |
| 2v初 |
对速度分解,由(2)问可知:tanα=
| vy |
| v初 |
| gt |
| v初 |
由上两式得 tanα=2tanθ
所以 tanα1=2tanθ=tanα2,
即证得 速度vB、vC与的方向平行
答:(1)小球从A到B的时间t1为
| 2v0tanθ |
| g |
(2)小球自第二次抛出到离斜面最远点所用的时间t2为
| 2v0tanθ |
| g |
(3)证明过程如上.
点评:本题就是对平抛运动规律的考查,平抛运动可以分解为在水平方向上的匀速直线运动,和竖直方向上的自由落体运动来求解.

练习册系列答案
相关题目
 如图所示,从足够长的斜面上A点,以水平速度v0抛出一个小球,不计空气阻力,它落到斜面上所用的时间为t1;若将此球改用2v0水平速度抛出,落到斜面上所用时间为t2,则t1:t2为( )
如图所示,从足够长的斜面上A点,以水平速度v0抛出一个小球,不计空气阻力,它落到斜面上所用的时间为t1;若将此球改用2v0水平速度抛出,落到斜面上所用时间为t2,则t1:t2为( ) 如图所示,从足够长的固定斜面的顶端
如图所示,从足够长的固定斜面的顶端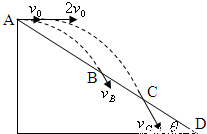
 如图所示,从足够长的斜面上A点,以水平速度v抛出一个小球,不计空气阻力,它落到斜面上所用的时间为t1;若将此球改用2v水平速度抛出,落到斜面上所用时间为t2,则t1:t2为( )
如图所示,从足够长的斜面上A点,以水平速度v抛出一个小球,不计空气阻力,它落到斜面上所用的时间为t1;若将此球改用2v水平速度抛出,落到斜面上所用时间为t2,则t1:t2为( )