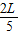题目内容
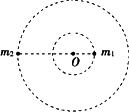
 如图所示,在远离其他天体的地方有两颗星球组成的双星,他们绕连线上的O点做匀速圆周运动,现测得两颗星之间的距离为L,质量之比m1:m2=3:2,则可知( )
如图所示,在远离其他天体的地方有两颗星球组成的双星,他们绕连线上的O点做匀速圆周运动,现测得两颗星之间的距离为L,质量之比m1:m2=3:2,则可知( )分析:双星靠相互间的万有引力提供向心力,具有相同的角速度.再根据万有引力定理即可求解.
解答:解:A.双星靠相互间的万有引力提供向心力,具有相同的角速度,根据T=
可知,周期之比为1:1,故A正确;
B.根据万有引力提供向心力,对m1有:G
=m1a1,对m2有:G
=m2a2,所以
=
=
,故B错误;
C.根据万有引力提供向心力,对m1有:G
=m1ω2r1,对m1有:G
=m2ω2r2,解得:m1r1=m2r2,
=
=
所以r1=
L,r2=
L,故C正确,D错误.
故选AC.
| 2π |
| ω |
B.根据万有引力提供向心力,对m1有:G
| m1m2 |
| L2 |
| m1m2 |
| L2 |
| a1 |
| a2 |
| m2 |
| m1 |
| 2 |
| 3 |
C.根据万有引力提供向心力,对m1有:G
| m1m2 |
| L2 |
| m1m2 |
| L2 |
| r1 |
| r2 |
| m2 |
| m1 |
| 2 |
| 3 |
| 2 |
| 5 |
| 3 |
| 5 |
故选AC.
点评:解决本题的关键知道双星靠相互间的万有引力提供向心力,具有相同的角速度.以及会用万有引力提供向心力进行求解.

练习册系列答案
相关题目
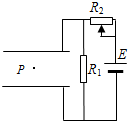 如图所示,在水平放置的平行板电容器之间,有一带电油滴P处于静止状态,若从某时刻起,油滴所带的电荷开始缓慢减小,为维持该油滴仍处于静止状态,可采取下列哪些措施( )
如图所示,在水平放置的平行板电容器之间,有一带电油滴P处于静止状态,若从某时刻起,油滴所带的电荷开始缓慢减小,为维持该油滴仍处于静止状态,可采取下列哪些措施( )