Question

【题目】在水平地面上放置着一半径为R的半圆形玻璃砖，直径AB与水平方向的夹角为45°，一束光线从C点水平射入玻璃砖中，OC= R，已知进入玻璃砖的光线第一次到达玻璃砖边缘时，恰好不从玻璃砖射出，求：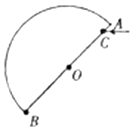

①玻璃的折射率；
②光线第一次从玻璃砖射出时的折射角．

Answer 1

【答案】解：①作出光路图如图．

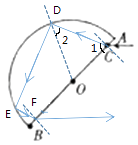
光在AB面发生折射时，由折射定律有：n=

光线在玻璃砖边缘恰好发生全反射，入射角∠2等于临界角C，则有：sin∠2=

在三角形AOD中，由正弦定理有： =

又∠1=90°﹣r，sin∠1=cosr=

联立解得玻璃的折射率为：n= ；∠2=45°

②由几何知识知，反射光线DE与DC垂直，光线射到E点时入射角等于∠2，也恰好发生全反射，反射光线EF与折射光线AD平行，光线在F点的入射角等于r，由光路可逆性原理可知，光线第一次从玻璃砖射出时的折射角等于45°．

答：①玻璃的折射率是 ；

②光线第一次从玻璃砖射出时的折射角是45°．

【解析】本题首先根据题意作出光路图．根据光在AB面折射，由折射定律列式．光线在玻璃砖边缘恰好发生全反射，入射角等于临界角C，由临界角公式．结合数学正弦定理列式，联立可求得玻璃的折射率；然后再由光的反射定律和几何关系求光线第一次从玻璃砖射出时的入射角，再由折射定律求得折射角，本题关键是作出光路图，同时要掌握全反射的条件和临界角公式，并结合几何知识求解相关角度．也要灵活运用光路可逆性原理。