题目内容
2. 如图所示,表面光滑的球A半径为R=10cm,其所受重力大小为80N,用长L=40cm的细线挂在竖直墙上(绳子延长线通过球心),球与墙之间夹着物体B,其厚H=20cm,物体B与墙之间的动摩擦因数μ=0.2.物块B在未脱离球A时沿墙匀速下滑,试求:
如图所示,表面光滑的球A半径为R=10cm,其所受重力大小为80N,用长L=40cm的细线挂在竖直墙上(绳子延长线通过球心),球与墙之间夹着物体B,其厚H=20cm,物体B与墙之间的动摩擦因数μ=0.2.物块B在未脱离球A时沿墙匀速下滑,试求:(1)球A对物块B的压力大小.
(2)物体B受的重力大小.
分析 (1)先对物体B受力分析,由共点力的平衡可得出小球受到的摩擦力大小,由滑动摩擦力公式可求压力的大小;
(2)对小球受力分析,由共点力的平衡条件可得出小球的重力.
解答 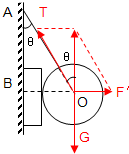 解:(1)设绳子拉力为T,B对A支持力为F′,则有:
解:(1)设绳子拉力为T,B对A支持力为F′,则有:
F′=mAgtanθ
tanθ=$\frac{H+R}{\sqrt{(L+R)^{2}-(H+R)^{2}}}$=0.75
解得:F′=60N
根据力的作用是相互的知,球A对物块B的压力大小为60N
(2)对物体B,竖直方向重力和墙面所给的摩擦力平衡,水平方向球A对物块B的
压力与墙面对物块B的支持力平衡.所以,有:
GB=μF′=0.2×60=12N
答:(1)球A对物块B的压力大小为60N.
(2)物体B受的重力大小为12N.
点评 本题考查共点力的平衡条件的应用,在解题时要注意灵活选取研究对象;同时注意动摩擦力的中的压力为垂直于接触面的压力,而不是重力.

练习册系列答案
 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案
相关题目
12.打点计时器是高中物理中重要的实验仪器,下图中的甲、乙两种打点计时器是高中物理实验中常用的,请回答下面的问题:

(1)图乙是电火花(填“电磁”或“电火花”)打点计时器,电源采用的是交流220V(填“交流4-6V”、“交流220V”、四节干电池).
(2)某同学在“探究小车速度随时间变化的规律”的实验中,用打点计时器记录了被小车拖动的纸带的运动情况,在纸带上确定出A、B、C、D、E、F、G共7个计数点,其相邻点间的距离如图丙所示,每两个相邻的计数点之间还有4个打印点未画出.
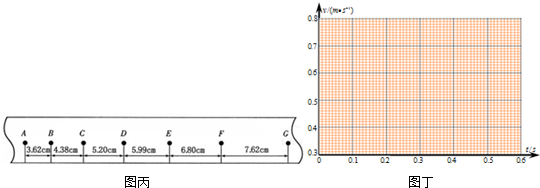
①试根据纸带上各个计数点间的距离,计算出打下B、F两个点时小车的瞬时速度,并将计算结果填入上表中,要求保留3位有效数字.
②将B、C、D、E、F各个时刻的瞬时速度标在直角坐标系中,并画出小车的瞬时速度随时间变化的关系图线.
③由所画速度-时间图象求出小车加速度为0.8m/s2.
④根据速度-时间图象判断,在打A计数点时,小车的速度vA=0.33m/s.
(3)打点计时器原来使用的电源的频率是50Hz,若在实验过程中交流电的频率为60Hz而未被发觉,这样计算出的加速度值与真实值相比将偏小(填“偏大”、“偏小”或“不变”).

(1)图乙是电火花(填“电磁”或“电火花”)打点计时器,电源采用的是交流220V(填“交流4-6V”、“交流220V”、四节干电池).
(2)某同学在“探究小车速度随时间变化的规律”的实验中,用打点计时器记录了被小车拖动的纸带的运动情况,在纸带上确定出A、B、C、D、E、F、G共7个计数点,其相邻点间的距离如图丙所示,每两个相邻的计数点之间还有4个打印点未画出.

| VB | VC | VD | VE | VF | |
| 数值 (m/s) | 0.479 | 0.560 | 0.640 |
②将B、C、D、E、F各个时刻的瞬时速度标在直角坐标系中,并画出小车的瞬时速度随时间变化的关系图线.
③由所画速度-时间图象求出小车加速度为0.8m/s2.
④根据速度-时间图象判断,在打A计数点时,小车的速度vA=0.33m/s.
(3)打点计时器原来使用的电源的频率是50Hz,若在实验过程中交流电的频率为60Hz而未被发觉,这样计算出的加速度值与真实值相比将偏小(填“偏大”、“偏小”或“不变”).
13.如图所示,静止在斜面上的物体所受重力的两个分力为F1、F2,下列正确的是( )
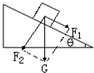

| A. | 因F1是重力的一个分力,所以F1也是物体受到的力 | |
| B. | F1是重力G沿斜面向下的分力,大小为Gsinθ | |
| C. | F2就是物体对斜面的正压力,大小为Gcosθ | |
| D. | 由于重力的存在,物体同时受到G、F1、F2的作用 |
10. 螺线管正中间的上方悬挂一个通有顺时针方向电流的小线圈,线圈的平面与螺线管的轴线在同一竖直面内,如图所示,当开关S合上时(一小段时间内),从上方俯视,线圈应该( )
螺线管正中间的上方悬挂一个通有顺时针方向电流的小线圈,线圈的平面与螺线管的轴线在同一竖直面内,如图所示,当开关S合上时(一小段时间内),从上方俯视,线圈应该( )
 螺线管正中间的上方悬挂一个通有顺时针方向电流的小线圈,线圈的平面与螺线管的轴线在同一竖直面内,如图所示,当开关S合上时(一小段时间内),从上方俯视,线圈应该( )
螺线管正中间的上方悬挂一个通有顺时针方向电流的小线圈,线圈的平面与螺线管的轴线在同一竖直面内,如图所示,当开关S合上时(一小段时间内),从上方俯视,线圈应该( )| A. | 顺时针方向转动,同时向左移动 | |
| B. | 逆时针方向转动,同时向右移动 | |
| C. | 顺时针方向转动,同时悬线的拉力减小 | |
| D. | 逆时针方向转动,同时悬线的拉力增大 |
17.下列说法正确的是( )
| A. | 摩擦力的方向一定与物体运动方向相反 | |
| B. | 摩擦力的大小一定与物体间的压力成正比 | |
| C. | 只要两物体间有摩擦力,就一定有弹力存在 | |
| D. | 形状规则的物体,重心一定在其几何中心 |
7.关于时刻和时间的说法中,正确的是( )
| A. | “第一节课是7点45分上课”这是指时间 | |
| B. | “前3秒”是指时刻 | |
| C. | “第4秒末和第5秒初”是指同一时刻 | |
| D. | “第3秒内”是时间,时间长度是3秒 |
14.下列几组物理量中,全部为矢量的一组是( )
| A. | 时间、位移 | B. | 速度、位移 | C. | 路程、质量 | D. | 长度、路程 |
11.航天飞机环绕地球做匀速圆周运动时,宇航员处于完全失重状态,下列说法中正确的是( )
| A. | 重力正好提供向心力 | B. | 宇航员不受重力作用 | ||
| C. | 宇航员不受任何力的作用 | D. | 宇航员受力平衡 |