题目内容
13. 如图所示,质量m=1kg的小球用细线拴住,线长l=0.5m,细线所受拉力达到F=18N时就会被拉断.当小球从图示位置释放后摆到悬点的正下方时,细线恰好被拉断.若此时小球距水平地面的高度h=5m,(g=10m/s2,P点在悬点的正下方)则下列选项中正确的是( )
如图所示,质量m=1kg的小球用细线拴住,线长l=0.5m,细线所受拉力达到F=18N时就会被拉断.当小球从图示位置释放后摆到悬点的正下方时,细线恰好被拉断.若此时小球距水平地面的高度h=5m,(g=10m/s2,P点在悬点的正下方)则下列选项中正确的是( )| A. | 细线刚好被拉断时小球的速度为2m/s | |
| B. | 细线断了之后小球再运动1s的时间落到地面 | |
| C. | 小球的落地点距P点3m | |
| D. | 小球落地时的速度大小为10m/s |
分析 小球摆到最低点时细线恰好被拉断,此时细线的拉力达到F=18N,由重力和拉力的合力提供向心力求出小球摆到最低点时的速度.细线被拉断后,小球做平抛运动,由高度h求出平抛运动的时间,再求解小球落地处到地面上P点的距离.
解答 解:A、摆到悬点正下方时,线恰好被拉断,说明此时线的拉力F=18 N,则由
F-mg=m$\frac{{v}^{2}}{l}$
可求得线断时球的水平速度为:v=$\sqrt{\frac{(F-mg)l}{m}}$=2 m/s,故A正确;
B、线断后球做平抛运动,由h=$\frac{1}{2}$gt2
可求得物体做平抛运动的时间为:t=$\sqrt{\frac{2h}{g}}=\sqrt{\frac{2×5}{10}}$s=1 s,故B正确;
C、平抛运动的水平位移为x=vt=2×1 m=2 m,故C错误;
D、根据动能定理得:$\frac{1}{2}m{{v}_{1}}^{2}-\frac{1}{2}m{v}^{2}=mgh$
解得:${v}_{1}=\sqrt{104}m/s$,故D错误.
故选:AB
点评 本题是向心力知识、牛顿第二定律和平抛运动知识的综合,关键要准确分析向心力的来源,熟练运用运动的分解法研究平抛运动.

练习册系列答案
相关题目
3.两电阻R1、R2的电流I和电压U的关系如图所示,以下正确的是( )


| A. | R1<R2 | |
| B. | R1=R2 | |
| C. | R1和R2串联后的总电阻的I-U图线应在区域Ⅲ | |
| D. | R1和R2并联后的总电阻的I-U图线应在区域Ⅱ |
1.从高为6m处静止释放一弹性小球,在与地面相碰后弹起,上升到高为3m处被拦截住,在这个过程中,关于小球位移的大小和路程的叙述中,正确是( )
| A. | 小球的位移大小为3m,方向竖直向下,路程为6m | |
| B. | 小球的位移大小为9m,方向竖直向上,路程为9m | |
| C. | 小球的位移大小为6m,方向竖直向上,路程为3m | |
| D. | 小球的位移大小为3m,方向竖直向下,路程为9m |
8.下列说法中,正确的是( )
| A. | 物体在恒力作用下一定作直线运动 | |
| B. | 曲线运动的速度方向时刻变化,但大小不一定变化 | |
| C. | 曲线运动的物体在某一点的速度方向是在这一点的受力方向 | |
| D. | 两个分运动是直线运动,则它们的合运动一定是直线运动 |
18.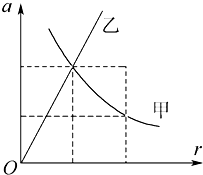 如图为甲、乙两球做匀速圆周运动时向心加速度随半径变化的关系图线,甲图线为双曲线的一支,乙图线为直线.由图象可以知道( )
如图为甲、乙两球做匀速圆周运动时向心加速度随半径变化的关系图线,甲图线为双曲线的一支,乙图线为直线.由图象可以知道( )
 如图为甲、乙两球做匀速圆周运动时向心加速度随半径变化的关系图线,甲图线为双曲线的一支,乙图线为直线.由图象可以知道( )
如图为甲、乙两球做匀速圆周运动时向心加速度随半径变化的关系图线,甲图线为双曲线的一支,乙图线为直线.由图象可以知道( )| A. | 甲球运动时,线速度的大小保持不变 | |
| B. | 甲球运动时,角速度的大小保持不变 | |
| C. | 乙球运动时,线速度的大小保持不变 | |
| D. | 乙球运动时,角速度的大小保持不变 |
2.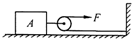 如图所示,用F=50N的水平拉力,通过一个动滑轮,使重为200N的物体A水平向右匀速移动了3m,在这个过程中( )
如图所示,用F=50N的水平拉力,通过一个动滑轮,使重为200N的物体A水平向右匀速移动了3m,在这个过程中( )
 如图所示,用F=50N的水平拉力,通过一个动滑轮,使重为200N的物体A水平向右匀速移动了3m,在这个过程中( )
如图所示,用F=50N的水平拉力,通过一个动滑轮,使重为200N的物体A水平向右匀速移动了3m,在这个过程中( )| A. | 拉力F做了150J的功 | B. | 拉力F做了300J的功 | ||
| C. | 重力做了600J的功 | D. | 重力做了1200J的功 |
 如图所示,摩托车做腾跃特技表演,以某一速度沿曲面冲上高0.8m、顶部水平的高台,若摩托车冲上高台的过程中始终以额定功率1.8kW行驶,经过1.2s到达平台顶部,到达顶部后立即关闭发动机油门,人和车落至地面时,恰能无碰撞地沿圆弧切线从A点切入光滑竖直圆弧轨道,并沿轨道下滑.已知圆弧半径为R=1.0m,人和车的总质量为180kg,圆弧轨道AOB所对应的圆心角为106°,特技表演的全过程中不计一切阻力,取g=10m/s2,sin53°=0.8,cos53°=0.6,求:
如图所示,摩托车做腾跃特技表演,以某一速度沿曲面冲上高0.8m、顶部水平的高台,若摩托车冲上高台的过程中始终以额定功率1.8kW行驶,经过1.2s到达平台顶部,到达顶部后立即关闭发动机油门,人和车落至地面时,恰能无碰撞地沿圆弧切线从A点切入光滑竖直圆弧轨道,并沿轨道下滑.已知圆弧半径为R=1.0m,人和车的总质量为180kg,圆弧轨道AOB所对应的圆心角为106°,特技表演的全过程中不计一切阻力,取g=10m/s2,sin53°=0.8,cos53°=0.6,求: 如图所示,滑板训练场地有一坡度较大的斜面AB,通过一小段弧形斜坡与地面连接.某运动员以一定的初速度冲上斜面,恰能滑到斜面的顶端B,然后又返回地面,如果忽略空气阻力和滑板与斜面间的摩擦力,下列速度v随时间t变化的图象中,能表示运动员在斜面AB上的运动情况是( )
如图所示,滑板训练场地有一坡度较大的斜面AB,通过一小段弧形斜坡与地面连接.某运动员以一定的初速度冲上斜面,恰能滑到斜面的顶端B,然后又返回地面,如果忽略空气阻力和滑板与斜面间的摩擦力,下列速度v随时间t变化的图象中,能表示运动员在斜面AB上的运动情况是( )


