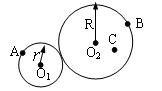题目内容
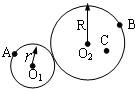 半径为r和R的圆柱体靠摩擦传动,已知R=2r,A、B分别在小圆柱与大圆柱的边缘上,C是圆柱体上的一点,O2C=r,如图所示,若两圆柱之间没有打滑现象,则
半径为r和R的圆柱体靠摩擦传动,已知R=2r,A、B分别在小圆柱与大圆柱的边缘上,C是圆柱体上的一点,O2C=r,如图所示,若两圆柱之间没有打滑现象,则vA:vB:vC=
2:2:1
2:2:1
TA:TC=1:2
1:2
.分析:两轮子靠摩擦传动,轮子边缘上的点线速度大小相同,同轴转动的点具有相同的角速度;应用ω=
可解线速度之比;再求得角速度之比,利用T=
即可求解.
| v |
| r |
| 2π |
| ω |
解答:解:传动过程中,两圆柱之间没有打滑现象,说明A、B两点的线速度相等,即vA=vB
B、C绕同一个轴转动,角速度相等,rB:rC=2:1
根据ω=
可知,vB:vC=2:1
所以vA:vB:vC=2:2:1
由A、C两点的半径和ω=
,求得三点的角速度之比为ωA:ωC=2:1:1;
由T=
得:TA:TC=2:1
故答案为:2:2:1; 1:2.
B、C绕同一个轴转动,角速度相等,rB:rC=2:1
根据ω=
| v |
| r |
所以vA:vB:vC=2:2:1
由A、C两点的半径和ω=
| v |
| r |
由T=
| 2π |
| ω |
故答案为:2:2:1; 1:2.
点评:解决本题的关键知道靠传送带传动轮子边缘上的点具有相同的线速度,共轴转动的点,具有相同的角速度,灵活应用ω=
和T=
求解.
| v |
| r |
| 2π |
| ω |

练习册系列答案
相关题目
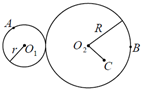 如图所示,半径为r和R的圆柱体靠摩擦传动,已知R=2r,A、B 分别在小圆柱与大圆柱的边缘上,O2C=r,若两圆柱之间没有打滑现象,则vA:vB:vC=
如图所示,半径为r和R的圆柱体靠摩擦传动,已知R=2r,A、B 分别在小圆柱与大圆柱的边缘上,O2C=r,若两圆柱之间没有打滑现象,则vA:vB:vC=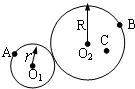 半径为r和R的圆柱体靠摩擦传动,已知R=2r,A、B分别在小圆柱与大圆柱的边缘上,C是圆柱体上的一点,O2C=r,如图所示,若两圆柱之间没有打滑现象,则vA:vB:vC=
半径为r和R的圆柱体靠摩擦传动,已知R=2r,A、B分别在小圆柱与大圆柱的边缘上,C是圆柱体上的一点,O2C=r,如图所示,若两圆柱之间没有打滑现象,则vA:vB:vC=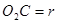 ,如图所示,若两圆柱之间没有打滑现象,则
,如图所示,若两圆柱之间没有打滑现象,则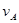 ∶
∶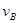 ∶
∶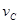 = _________,
= _________,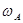 ∶
∶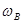 ∶
∶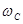 =__________
=__________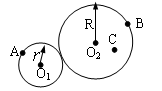
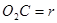 ,如图所示,若两圆柱之间没有打滑现象,则
,如图所示,若两圆柱之间没有打滑现象,则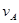 ∶
∶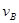 ∶
∶ = _________,
= _________, ∶
∶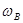 ∶
∶ =__________
=__________