题目内容
12.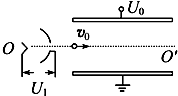 真空中的某装置如图所示,现有质子、氘核和α粒子都从O点由静止释放,经过相同加速电场和偏转电场,射出后都打在同一个与OO′垂直的荧光屏上,使荧光屏上出现亮点(已知质子、氘核和α粒子质量之比为1:2:4,电量之比为1:1:2,重力不计).下列说法中正确的是( )
真空中的某装置如图所示,现有质子、氘核和α粒子都从O点由静止释放,经过相同加速电场和偏转电场,射出后都打在同一个与OO′垂直的荧光屏上,使荧光屏上出现亮点(已知质子、氘核和α粒子质量之比为1:2:4,电量之比为1:1:2,重力不计).下列说法中正确的是( )| A. | 偏转电场的电场力对三种粒子做功之比为1:1:2 | |
| B. | 三种粒子在偏转电场中运动时间之比为2:1:1 | |
| C. | 三种粒子出偏转电场时的速度相同 | |
| D. | 三种粒子的运动轨迹相同 |
分析 根据动能定理求出粒子进入偏转电场时的速度,抓住在偏转电场中垂直于电场方向做匀速直线运动,求出运动的时间.结合竖直方向上做匀加速直线运动,求出出电场时竖直方向上的分速度以及偏转的位移,从而可判断三个粒子打在屏光荧上的位置.根据动能定理求出偏转电场电场力做功的大小关系.
解答 解:在加速电场中,由动能定理得:qU1=$\frac{1}{2}$m${v}_{0}^{2}$-0,在偏转电场中,偏转位移y=$\frac{1}{2}$at2=$\frac{1}{2}$•$\frac{q{U}_{2}}{md}$•$\frac{{L}^{2}}{{v}_{0}^{2}}$,联立得y=$\frac{{U}_{2}{L}^{2}}{4{U}_{1}d}$,可见y与粒子的电量和质量无关,则三种粒子的偏转位移相等,运动轨迹相同.
由上可得:进入偏转电场的速度v0=$\sqrt{\frac{2q{U}_{1}}{m}}$,因为质子、氘核和α粒子的比荷之比为2:1:1,则初速度之比$\sqrt{2}$:1:1,在在偏转电场中运动时间t=$\frac{L}{{v}_{0}}$,则知时间之比为1:$\sqrt{2}$:$\sqrt{2}$
偏转电场的电场力对粒子做功W=qEy,因为E和y相同,电量之比为1:1:2,则电场力做功为1:1:2.故AD正确,BC错误.
故选:AD
点评 本题考查粒子在电场中的加速和偏转,掌握处理粒子在电场中偏转的方法,知道粒子在垂直电场和沿电场方向上的运动规律,抓住等时性,结合运动学公式进行求解.

练习册系列答案
相关题目
2.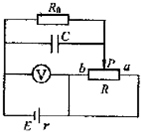 如图所示、电源的电动势和内阻分别为E、r,滑动变阻器的滑片由b向a缓慢移动的过程中(不考虑电容器充放电对电路的影响),下列各物理量变化情况为( )
如图所示、电源的电动势和内阻分别为E、r,滑动变阻器的滑片由b向a缓慢移动的过程中(不考虑电容器充放电对电路的影响),下列各物理量变化情况为( )
 如图所示、电源的电动势和内阻分别为E、r,滑动变阻器的滑片由b向a缓慢移动的过程中(不考虑电容器充放电对电路的影响),下列各物理量变化情况为( )
如图所示、电源的电动势和内阻分别为E、r,滑动变阻器的滑片由b向a缓慢移动的过程中(不考虑电容器充放电对电路的影响),下列各物理量变化情况为( )| A. | 电源的热功率先减少后增加 | B. | 电容器所带电荷量先增加后减少 | ||
| C. | 电源的输出功率先减少后增加 | D. | 电压表的读数先减少后增加 |
3. 带电粒子射人一固定的带正电的点电荷Q的电场中,沿图中实线轨迹从a运动到b,a、b两点到点电荷Q的距离分别为ra、rb(ra>rb),不计粒子的重力,则可知( )
带电粒子射人一固定的带正电的点电荷Q的电场中,沿图中实线轨迹从a运动到b,a、b两点到点电荷Q的距离分别为ra、rb(ra>rb),不计粒子的重力,则可知( )
 带电粒子射人一固定的带正电的点电荷Q的电场中,沿图中实线轨迹从a运动到b,a、b两点到点电荷Q的距离分别为ra、rb(ra>rb),不计粒子的重力,则可知( )
带电粒子射人一固定的带正电的点电荷Q的电场中,沿图中实线轨迹从a运动到b,a、b两点到点电荷Q的距离分别为ra、rb(ra>rb),不计粒子的重力,则可知( )| A. | 运动粒子带负电 | |
| B. | a到b的过程中,电场力对粒子不做功 | |
| C. | b点的场强大于a点的场强 | |
| D. | a到b的过程中,电场力对粒子做的功等于带电粒子动能的变化 |
20. 利用传感器和计算机可以研究力的大小变化的情况,实验时让某消防队员从平台上跳下,自由下落H后双脚触地,他顺势弯曲双腿,他的重心又下降了h.计算机显示消防队员受到地面支持力F随时间变化图象如图所示.根据图象提供的信息,以下判断不正确的是( )
利用传感器和计算机可以研究力的大小变化的情况,实验时让某消防队员从平台上跳下,自由下落H后双脚触地,他顺势弯曲双腿,他的重心又下降了h.计算机显示消防队员受到地面支持力F随时间变化图象如图所示.根据图象提供的信息,以下判断不正确的是( )
 利用传感器和计算机可以研究力的大小变化的情况,实验时让某消防队员从平台上跳下,自由下落H后双脚触地,他顺势弯曲双腿,他的重心又下降了h.计算机显示消防队员受到地面支持力F随时间变化图象如图所示.根据图象提供的信息,以下判断不正确的是( )
利用传感器和计算机可以研究力的大小变化的情况,实验时让某消防队员从平台上跳下,自由下落H后双脚触地,他顺势弯曲双腿,他的重心又下降了h.计算机显示消防队员受到地面支持力F随时间变化图象如图所示.根据图象提供的信息,以下判断不正确的是( )| A. | t2时刻消防队员重心向下运动的速度最大 | |
| B. | t4时刻消防队员的动能为零 | |
| C. | t2时刻消防队员的重力势能最小 | |
| D. | 在t1至t4时间内,消防队员的机械能在减少 |
7.物体沿一条直线运动,下列说法正确的是( )
| A. | 物体在某时刻的速度是3 m/s,则物体在1 s内一定走3m | |
| B. | 物体在某1 s内的平均速度是3 m/s,则物体在这1 s内的位移一定是3m | |
| C. | 物体在某段时间内的平均速度是3 m/s,则物体在1 s内的位移一定是3m | |
| D. | 物体在某段位移内的平均速度为3 m/s,则物体在通过这段位移一半时的速度一定是1.5 m/s |
17.一遥控玩具小车在平直路上运动的位移-时间图象,如图所示,则( )


| A. | 0-10s汽车的速度为3m/s | B. | 0-15 s内汽车的位移为300 m | ||
| C. | 0-25s内汽车做单方向直线运动 | D. | 20s末汽车的速度大小为1m/s |
1.下列说法正确的是( )
| A. | 电流方向就是电荷定向移动的方向 | |
| B. | 由公式R=$\frac{U}{I}$可知,电阻R与电压U成正比,与电流I成反比 | |
| C. | I-U图象是过原点的一条直线的元件是线性元件 | |
| D. | 利用金属的电阻率随温度的升高而增大可以制成电阻温度计 |
 如图,光滑绝缘半球槽的半径为R,处在水平向右的匀强电场中,一质量为m的带电小球从槽的右端A处无初速沿轨道滑下,滑到最低点B时,球对轨道的压力为1.5mg.求
如图,光滑绝缘半球槽的半径为R,处在水平向右的匀强电场中,一质量为m的带电小球从槽的右端A处无初速沿轨道滑下,滑到最低点B时,球对轨道的压力为1.5mg.求