题目内容
3.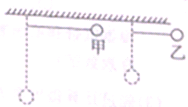 甲、乙两球质量相同,悬线甲长乙短,如果将两球由同一水平面无初速度释放,如图所示,不计空气阻力,则两球通过最低点位置时,下列说法中正确的是( )
甲、乙两球质量相同,悬线甲长乙短,如果将两球由同一水平面无初速度释放,如图所示,不计空气阻力,则两球通过最低点位置时,下列说法中正确的是( )| A. | 甲球的动能比乙球小 | |
| B. | 两球受到的拉力大小相等 | |
| C. | 两球的向心加速度大小不相等 | |
| D. | 相对同一参考平面,两球机械能相等 |
分析 根据动能定理即可求解A答案,根据圆周运动向心力公式及动能定理即可求得B答案,根据向心力公式即可求解C答案,由重力做功多少,重力势能就减少多少,分析D项.
解答 解:A、从同一水平面无初速释放到小球通过最低点的过程中运用动能定理可知:小球的末动能等于小球重力所做的功,而由题意可知甲下落的位移大,故甲球重力做的功多,故甲球的动能大于乙球的动能,故A错误;
B、在最低点有:F-mg=m$\frac{{v}^{2}}{l}$,根据动能定理得:$\frac{1}{2}m{v}^{2}$=mgl,解得:F=3mg,与绳长无关,故B正确;
C、通过最低点时,两球的向心加速度为:a=$\frac{{v}^{2}}{l}$=2g,与绳长无关,故C错误;
D、相对同一参考平面,两球开始时的重力势能相等;因机械能守恒;则两球机械能相等;故D正确;
故选:BD.
点评 本题主要考查了动能定理、圆周运动向心力公式及向心加速度公式、机械能守恒定律得应用;要注意根据机械能守恒定律推导BC两项,并可以作为结论应用.

练习册系列答案
相关题目
14.某物体在从A点运动到B点的过程中,克服重力做功为3J,拉力做功1J,克服空气阻力做功为0.5J,则在A点的( )
| A. | 重力势能比B点大3J | B. | 机械能比B点小1J | ||
| C. | 动能比B点大2.5J | D. | 机械能比B点小0.5J |
11.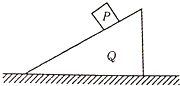 如图,小物块P位于光滑斜面上,斜面Q位于光滑水平地面上,小物块P从静止开始沿斜面下滑的过程中( )
如图,小物块P位于光滑斜面上,斜面Q位于光滑水平地面上,小物块P从静止开始沿斜面下滑的过程中( )
 如图,小物块P位于光滑斜面上,斜面Q位于光滑水平地面上,小物块P从静止开始沿斜面下滑的过程中( )
如图,小物块P位于光滑斜面上,斜面Q位于光滑水平地面上,小物块P从静止开始沿斜面下滑的过程中( )| A. | 斜面Q静止不动 | |
| B. | 小物块P对斜面Q的弹力对斜面做正功 | |
| C. | 小物块P的机械能守恒 | |
| D. | 斜面Q对小物块P的弹力方向与接触面不垂直 |
8.下列说法正确的是( )
| A. | 最先提出“所有行星的轨道的半长轴的三次方跟它的公转周期的二次方的比值都相等”观点的科学家是哈雷 | |
| B. | 最先用实验方法测出引力常量的科学家是牛顿 | |
| C. | 牛顿运动定律是经典力学的基础 | |
| D. | 经典力学可以解决自然界中的所有问题 |
12. 如图是平抛竖落仪,用小锤打击弹性金属片,金属片把a球沿水平方向抛出,同时b球松开自由落下,两球质量相等,不计一切阻力,则( )
如图是平抛竖落仪,用小锤打击弹性金属片,金属片把a球沿水平方向抛出,同时b球松开自由落下,两球质量相等,不计一切阻力,则( )
 如图是平抛竖落仪,用小锤打击弹性金属片,金属片把a球沿水平方向抛出,同时b球松开自由落下,两球质量相等,不计一切阻力,则( )
如图是平抛竖落仪,用小锤打击弹性金属片,金属片把a球沿水平方向抛出,同时b球松开自由落下,两球质量相等,不计一切阻力,则( )| A. | b球比a球先落地 | |
| B. | 下落相同高度时,a求速率比b球速率大 | |
| C. | a球在水平和竖直方向的运动相互没有影响 | |
| D. | 两球之所以同时落地是因为在竖直方向上都是自由落体运动 |
13. 如图所示,一质量为m的物体在沿斜面向上的恒力F作用下,由静止从底端向上做匀加速直线运动.若斜面足够长,表面光滑,倾角为θ.经时间t恒力F做功80J,此后撤去恒力F,物体又经时间t回到出发点,且回到出发点时的速度大小为v,若以地面为重力势能的零势能面,则下列说法中正确的是( )
如图所示,一质量为m的物体在沿斜面向上的恒力F作用下,由静止从底端向上做匀加速直线运动.若斜面足够长,表面光滑,倾角为θ.经时间t恒力F做功80J,此后撤去恒力F,物体又经时间t回到出发点,且回到出发点时的速度大小为v,若以地面为重力势能的零势能面,则下列说法中正确的是( )
 如图所示,一质量为m的物体在沿斜面向上的恒力F作用下,由静止从底端向上做匀加速直线运动.若斜面足够长,表面光滑,倾角为θ.经时间t恒力F做功80J,此后撤去恒力F,物体又经时间t回到出发点,且回到出发点时的速度大小为v,若以地面为重力势能的零势能面,则下列说法中正确的是( )
如图所示,一质量为m的物体在沿斜面向上的恒力F作用下,由静止从底端向上做匀加速直线运动.若斜面足够长,表面光滑,倾角为θ.经时间t恒力F做功80J,此后撤去恒力F,物体又经时间t回到出发点,且回到出发点时的速度大小为v,若以地面为重力势能的零势能面,则下列说法中正确的是( )| A. | 物体回到出发点时的机械能是80 J | |
| B. | 在撤去力F前的瞬间,力F的功率是$\frac{2}{3}$mgvsinθ | |
| C. | 撤去力F前的运动过程中,物体的重力势能一直在增加,撤去力F后的运动过程中物体的重力势能一直在减少 | |
| D. | 撤去力F前的运动过程中,物体的动能一直在增加,撤去力F后的运动过程中物体的动能一直在减少 |

 如图所示,让小球从图中的C位置由静止开始摆下,摆到最低点D处,摆线刚好从与小球拴接处被拉断,并立即撤去摆线,小球在粗糙的水平面上由D点向D做匀减速运动,到达小孔A进入半径R=0.3m的竖直放置的光滑竖直圆弧轨道,当小球进入圆轨道立即关闭A孔,已知摆线长L=2m,θ=60°,小球质量为m=0.5kg,小球与粗糙水平面动摩擦因数μ=$\frac{1}{8}$,g取10m/s2.求:
如图所示,让小球从图中的C位置由静止开始摆下,摆到最低点D处,摆线刚好从与小球拴接处被拉断,并立即撤去摆线,小球在粗糙的水平面上由D点向D做匀减速运动,到达小孔A进入半径R=0.3m的竖直放置的光滑竖直圆弧轨道,当小球进入圆轨道立即关闭A孔,已知摆线长L=2m,θ=60°,小球质量为m=0.5kg,小球与粗糙水平面动摩擦因数μ=$\frac{1}{8}$,g取10m/s2.求: 某学生在做“研究平抛物体运动”的实验中,得到了如图所示物体的运动轨迹.若按图示方法建立平面直角坐标系,A、B、C三点的坐标值分别如图所示,则:
某学生在做“研究平抛物体运动”的实验中,得到了如图所示物体的运动轨迹.若按图示方法建立平面直角坐标系,A、B、C三点的坐标值分别如图所示,则: