题目内容
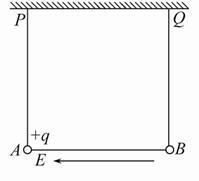
如图所示，有三根长度均为L=0.3 m的不可伸长的绝缘细线，其中两根的一端分别固定在天花板上的P、Q点，另一端分别拴有质量均为m=0.12 kg的带电小球A和B，其中A球带正电，电荷量为q=3×10-6 C。A、B之间用第三根线连接起来。在水平向左的匀强电场E作用下，A、B保持静止，悬线仍处于竖直方向，且A、B间细线恰好伸直。(静电力常量k=9×109 N·m2/C2，取g=10 m/s2)
(1)此匀强电场的电场强度E为多大；
(2)现将PA之间的线烧断，由于有空气阻力，A、B球最后会达到新的平衡位置。求此时细线QB所受的拉力FT的大小，并求出A、B间细线与竖直方向的夹角θ；
(3)求A球的电势能与烧断前相比改变了多少(不计B球所带电荷对匀强电场的影响)。
【解析】(1)B球水平方向合力为零，则有
(2分)
所以
(2分)
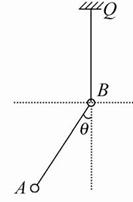
(2)两球及细线最后位置如图所示，
QB的拉力FT=2mg=2×0.12×10 N=2.4 N (2分)
A球受力平衡，则有qE=mgtanθ, (2分)
所以
，即θ=37° (2分)
(3)A球克服电场力做功，
W=-qEL(1-sinθ)=-3×10-6×3×105×0.3×(1-0.6) J=-0.108 J (3分)
所以A球的电势能增加了ΔEp=0.108 J (2分)
答案：(1)3×105 N/C (2)2.4 N 37°
(3)增加0.108 J
练习册系列答案
相关题目
； 
；
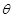