题目内容
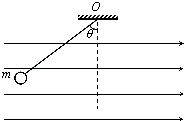 如图所示,一带电小球质量m=1kg,用长度L=1m绝缘细线悬挂在水平向右的匀强电场中,静止时悬线与竖直方向成θ=53°,已知sin53°=0.8,cos53°=0.6,取重力加速度g=10m/s2.
如图所示,一带电小球质量m=1kg,用长度L=1m绝缘细线悬挂在水平向右的匀强电场中,静止时悬线与竖直方向成θ=53°,已知sin53°=0.8,cos53°=0.6,取重力加速度g=10m/s2.(1)求小球所受的电场力的大小F;
(2)若仅将电场强度大小突然减小为原来的
| 1 | 3 |
分析:(1)小球静止,由平衡条件可以求出电场力;
(2)由动能定理求出小球到达最低点时的速度,由牛顿第二定律可以求出细线对小球的拉力.
(2)由动能定理求出小球到达最低点时的速度,由牛顿第二定律可以求出细线对小球的拉力.
解答:解:(1)小球静止,处于平衡状态,
由平衡条件可得,电场力F=mgtan53°=
mg≈13.3N;
(2)小球从静止到摆到最低点的过程中,
由动能定理得:mgL(1-cos53°)-
Lsin53°=
mv2-0,解得:v=2m/s;
在最低点,由牛顿第二定律得:T-mg=m
,
解得:T=14N;
答:(1)小球所受的电场力的大小为13.3N;
(2)若仅将电场强度大小突然减小为原来的
,求小球摆到最低点时的速度大小υ和细线对小球的拉力大小为14N.
由平衡条件可得,电场力F=mgtan53°=
| 4 |
| 3 |
(2)小球从静止到摆到最低点的过程中,
由动能定理得:mgL(1-cos53°)-
| F |
| 3 |
| 1 |
| 2 |
在最低点,由牛顿第二定律得:T-mg=m
| v2 |
| L |
解得:T=14N;
答:(1)小球所受的电场力的大小为13.3N;
(2)若仅将电场强度大小突然减小为原来的
| 1 |
| 3 |
点评:本题考查了求细线的拉力,应用平衡条件、动能定理、牛顿第二定律即可正确解题.

练习册系列答案
相关题目
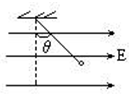 如图所示,一带电小球用丝线悬挂在水平方向的匀强电场中,当小球静止后把悬线烧断,则小球在电场中将做( )
如图所示,一带电小球用丝线悬挂在水平方向的匀强电场中,当小球静止后把悬线烧断,则小球在电场中将做( ) 如图所示,一带电小球以v0=10m/s的初速度冲上一倾角为37°的光滑斜面,斜面处在水平向右的匀强电场E中.已知小球受到的电场力是重力的一半,则小球从开始到再返回斜面底端的时间可能是( )(sin37°=0.6,cos37°=0.8.)
如图所示,一带电小球以v0=10m/s的初速度冲上一倾角为37°的光滑斜面,斜面处在水平向右的匀强电场E中.已知小球受到的电场力是重力的一半,则小球从开始到再返回斜面底端的时间可能是( )(sin37°=0.6,cos37°=0.8.) 如图所示,一带电小球从A处竖直向上进入一水平方向的匀强电场中,进入电场时小球的动能为6J,运动到最高点B时小球的动能为10J,则小球运动到与A点在同一水平面上的C点(图中未画出)时的动能为( )
如图所示,一带电小球从A处竖直向上进入一水平方向的匀强电场中,进入电场时小球的动能为6J,运动到最高点B时小球的动能为10J,则小球运动到与A点在同一水平面上的C点(图中未画出)时的动能为( )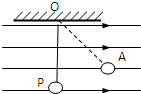 如图所示,一带电小球的质量m=2×10-4kg,用长为L=0.8m的细线悬挂在水平方向的匀强电场中O点,场强E=3×104N/C,当细线与竖直方向夹角为θ=37°时,摆球恰好静止在A点.(g=10m/s2,sin37°=0.6,cos37°=0.8)
如图所示,一带电小球的质量m=2×10-4kg,用长为L=0.8m的细线悬挂在水平方向的匀强电场中O点,场强E=3×104N/C,当细线与竖直方向夹角为θ=37°时,摆球恰好静止在A点.(g=10m/s2,sin37°=0.6,cos37°=0.8)