题目内容
如图所示，平板小车沿水平地面始终以加速度a做匀加速直线运动．当小车速度增至v时，将一小物块无初速地放于平板小车的A端（小车的加速度保持不变）．物块与小车间的动摩擦因数为μ，（μg＞a），要使物块不会从小车上滑出，求平板小车的最小长度L0．
解：设物块的质量为m，经过时间t物块运动到小车B端，物块的末速度和位移分别为v1=
x1=
t2=μgt2时间t内小车的位移和末速度分别为
v2=v+at
x2=vt+
at2若物块刚好未从小车B端滑出，则有
v1=v2
x2=x1+L0（如图所示）
即：μgt=v+at
vt+
at2=μgt2+L0解得：
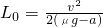
即平板小车的最小长度为
．分析：物块放上平板小车后，对物块受力分析后求出其加速度，可知其加速度大于平板小车的加速度，加速物块恰好不掉下来，则物块运动到平板小车的最左端时，两者速度应该相等，根据运动学公式联立方程求解即可．
点评：本题关键抓住物块恰好不掉下来的临界情况，根据运动学公式联立方程求解．
练习册系列答案
相关题目
如图所示，平板小车沿水平地面始终以加速度a做匀加速直线运动．当小车速度增至v时，将一小物块无初速地放于平板小车的A端（小车的加速度保持不变）．物块与小车间的动摩擦因数为μ，（μg＞a），要使物块不会从小车上滑出，求平板小车的最小长度L0．
