题目内容
 在竖直平面内有一个光滑的半圆轨道,轨道两端连线即直径在竖直方向,轨道半径为0.9m,一个质量为0.5kg的小球以一定的初速度滚上轨道(取g=10m/s2).求:
在竖直平面内有一个光滑的半圆轨道,轨道两端连线即直径在竖直方向,轨道半径为0.9m,一个质量为0.5kg的小球以一定的初速度滚上轨道(取g=10m/s2).求:(1)小球在最高点不脱离轨道的最小速率是多少?
(2)小球在最高点速率v=4m/s时,小球对轨道的压力是多少?
分析:(1)小球在最高点不脱离轨道的条件是重力不大于小球做圆周运动所需要的向心力,当只由重力提供向心力时,速度最小,根据牛顿第二定律列式求出最小速率.
(2)小球在最高点速率v=4m/s时,由重力和轨道的压力的合力提供向心力,列式求出轨道对小球的压力,再根据牛顿第三定律得到小球对轨道的压力.
(2)小球在最高点速率v=4m/s时,由重力和轨道的压力的合力提供向心力,列式求出轨道对小球的压力,再根据牛顿第三定律得到小球对轨道的压力.
解答:解(1)在最高点小球不脱离轨道的条件是重力不大于小球做圆周运动所需要的向心力,即:
mg≤m
则所求的最小速率:
vmin=
=
m/s=3m/s
(2)因为v=4m/s>vmin,所以轨道对小球有一定的压力F.
则根据牛顿第二定律得:F+mg=m
所以 F=m(
-g)=0.5×(
-10)N≈3.9N
由牛顿第三定律知,小球对轨道的压力为:F′=F=3.5N
答:(1)小球在最高点不脱离轨道的最小速率是3m/s.
(2)小球在最高点速率v=4m/s时,小球对轨道的压力是3.5N.
mg≤m
| v2 |
| R |
则所求的最小速率:
vmin=
| gR |
| 0.9×10 |
(2)因为v=4m/s>vmin,所以轨道对小球有一定的压力F.
则根据牛顿第二定律得:F+mg=m
| v2 |
| R |
所以 F=m(
| v2 |
| R |
| 42 |
| 0.9 |
由牛顿第三定律知,小球对轨道的压力为:F′=F=3.5N
答:(1)小球在最高点不脱离轨道的最小速率是3m/s.
(2)小球在最高点速率v=4m/s时,小球对轨道的压力是3.5N.
点评:本题与轻绳的模型类似,关键分析小球的受力,确定什么力提供向心力,运用牛顿运动定律研究圆周运动动力学问题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
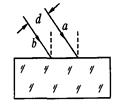
 在空气中水平放置着一个长方体玻璃砖.在竖直平面内有两束单色光,如图所示,其中a为紫光、b为红光,两束光相互平行且相距为d,斜射到长方体玻璃砖的上表面,折射后直接射到下表面,然后射出.则下列说法中可能发生的是( )
在空气中水平放置着一个长方体玻璃砖.在竖直平面内有两束单色光,如图所示,其中a为紫光、b为红光,两束光相互平行且相距为d,斜射到长方体玻璃砖的上表面,折射后直接射到下表面,然后射出.则下列说法中可能发生的是( )| A、两束光射出玻璃砖后仍然平行,距离小于d | B、两束光射出玻璃砖后仍然平行,距离等于d | C、两束光射出玻璃砖后不会沿同一路径传播 | D、两束光射出玻璃砖后将不再平行 |
在空气中水平放置着一个长方体玻璃砖。在竖直平面内有两束单色光,如图所示,其中a为紫光、b为红光,两束光相互平行且相距为d,斜射到长方体玻璃砖的上表面,折射后直接射到下表面,然后射出。则下列说法中可能发生的是( )
| A.两束光射出玻璃砖后仍然平行,距离小于d |
| B.两束光射出玻璃砖后仍然平行,距离等于d |
| C.两束光射出玻璃砖后不会沿同一路径传播 |
| D.两束光射出玻璃砖后将不再平行 |
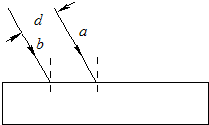 如图所示,在折射率大于玻璃折射率的透明液体中,水平放置着一个长方体玻璃砖.在竖直平面内有两束光线,相互平行、相距为d,斜射到长方体的上表面上,折射后直接射到下表面,然后射出.已知图中a为红光、b为紫光,则( )
如图所示,在折射率大于玻璃折射率的透明液体中,水平放置着一个长方体玻璃砖.在竖直平面内有两束光线,相互平行、相距为d,斜射到长方体的上表面上,折射后直接射到下表面,然后射出.已知图中a为红光、b为紫光,则( )