题目内容
18.一质点做匀变速直线运动,初速度为1m/s,末速度为5m/s,通过位移为60m.求:(1)运动过程中的加速度
(2)此运动过程的时间.
分析 (1)知道物体运动的初速度和末速度和位移,根据速度时间的关系式可以直接计算加速度的大小;
(2)根据速度时间的关系式计算时间的大小.
解答 解:(1)根据${v}^{2}-{v}_{0}^{2}=2ax$得:
a=$\frac{{v}^{2}-{v}_{0}^{2}}{2x}=\frac{{5}^{2}-{1}^{2}}{2×60}$=0.2m/s2;
(2)根据v=v0+at得:
t=$\frac{v-{v}_{0}^{\;}}{a}=\frac{5-1}{0.2}$=20s;
答:(1)运动过程中的加速度为0.2m/s2;
(2)此运动过程的时间为20s.
点评 解决本题的关键掌握匀变速直线运动的速度时间公式和速度时间的关系式.直接就计算即可.

练习册系列答案
相关题目
8.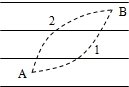 如图所示,平行线代表电场线,但未标明方向,一个电子在电场力作用下,当它由A点运动到B点时动能减少了10ev,则以下判断正确的是( )
如图所示,平行线代表电场线,但未标明方向,一个电子在电场力作用下,当它由A点运动到B点时动能减少了10ev,则以下判断正确的是( )
 如图所示,平行线代表电场线,但未标明方向,一个电子在电场力作用下,当它由A点运动到B点时动能减少了10ev,则以下判断正确的是( )
如图所示,平行线代表电场线,但未标明方向,一个电子在电场力作用下,当它由A点运动到B点时动能减少了10ev,则以下判断正确的是( )| A. | 电子的运动轨迹如图中的虚线1所示 | |
| B. | 电子的运动轨迹如图中的虚线2所示 | |
| C. | 电场线的方向水平向左 | |
| D. | 电场线的方向水平向右 |
9.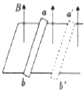 如图所示,水平放置且电阻不计的光滑金属导轨处于竖直向上的匀强磁场中,阻值为R的导体棒在外力F的作用下,从位置ab由静止开始匀加速直线运动到位置a′b′,若先、后两次导体棒运动的加速度之比为1:2,则在先、后两次导体棒的运动过程中( )
如图所示,水平放置且电阻不计的光滑金属导轨处于竖直向上的匀强磁场中,阻值为R的导体棒在外力F的作用下,从位置ab由静止开始匀加速直线运动到位置a′b′,若先、后两次导体棒运动的加速度之比为1:2,则在先、后两次导体棒的运动过程中( )
 如图所示,水平放置且电阻不计的光滑金属导轨处于竖直向上的匀强磁场中,阻值为R的导体棒在外力F的作用下,从位置ab由静止开始匀加速直线运动到位置a′b′,若先、后两次导体棒运动的加速度之比为1:2,则在先、后两次导体棒的运动过程中( )
如图所示,水平放置且电阻不计的光滑金属导轨处于竖直向上的匀强磁场中,阻值为R的导体棒在外力F的作用下,从位置ab由静止开始匀加速直线运动到位置a′b′,若先、后两次导体棒运动的加速度之比为1:2,则在先、后两次导体棒的运动过程中( )| A. | 运动到相同位置时的外力F之比为1:2 | |
| B. | 运动到相同位置时导体棒受到的安培力之比为1:2 | |
| C. | 电流的平均值之比为1:$\sqrt{2}$ | |
| D. | 通过任一截面的电荷量之比为1:2 |
 如图所示,真空中有两个点电荷A,B,它们固定在一条直线上相距L=0.3m的两点,它们的电荷量分别为QA=16×10-12C,QB=4.0×10-12C,现引入第三个同种点电荷C.
如图所示,真空中有两个点电荷A,B,它们固定在一条直线上相距L=0.3m的两点,它们的电荷量分别为QA=16×10-12C,QB=4.0×10-12C,现引入第三个同种点电荷C.
 如图所示为某轻弹簧在弹性限度内所受拉力F与伸长量x之间关系的图象.求:
如图所示为某轻弹簧在弹性限度内所受拉力F与伸长量x之间关系的图象.求: