题目内容
13. 如图所示,粗糙斜面固定于光滑的半圆轨道平滑相接,半圆轨道半径为R,当小球自斜面上 h=2R高处某点无初速滑下进入半圆轨道时,小球达到半圆轨道的最大轨道为R,若要使小球恰好能通过半圆的最高点,则小球的释放轨道为( )
如图所示,粗糙斜面固定于光滑的半圆轨道平滑相接,半圆轨道半径为R,当小球自斜面上 h=2R高处某点无初速滑下进入半圆轨道时,小球达到半圆轨道的最大轨道为R,若要使小球恰好能通过半圆的最高点,则小球的释放轨道为( )| A. | 4R | B. | 4.5R | ||
| C. | 5R | D. | 条件不足,无法确定 |
分析 先运用动能定理对小球从h=2R高处滑下的过程列方程.要使小球恰好能通过半圆的最高点,由重力提供向心力,列式求出最高点的速度.再由动能定理列式,即可解得.
解答 解:设小球在斜面上所受的摩擦力大小为f,斜面的倾角为α.
对第一种情况,由动能定理得:mgR-f•$\frac{2R}{sinα}$=0
对第二种情况:
在最高点有,mg=m$\frac{{v}^{2}}{R}$
由动能定理得 mg(h′-2R)-f•$\frac{h′}{sinα}$=$\frac{1}{2}m{v}^{2}$
联立解得 h′=5R
故选:C.
点评 本题是动能定理与向心力的综合,要注意挖掘隐含的临界条件:小球恰好能通过半圆的最高点时由重力提供向心力.

练习册系列答案
相关题目
3.如图是某辆汽车的速度表.汽车起动后经过3s,速度表的指针指在图示位置.由表可知( )


| A. | 此时汽车的瞬时速度是60m/s | |
| B. | 此时汽车的瞬时速度是60km/h | |
| C. | 起动后3s内汽车的平均速度是60m/s | |
| D. | 起动后3s内汽车的平均速度是60km/h |
4. 如图所示,乒乒乘坐速度为0.8c(c为光速)的宇宙飞船追赶正前方的宝宝,宝宝的飞行速度为0.6c,乒乒向宝宝发出一束光进行联络,则宝宝观测到该光束的传播速度为( )
如图所示,乒乒乘坐速度为0.8c(c为光速)的宇宙飞船追赶正前方的宝宝,宝宝的飞行速度为0.6c,乒乒向宝宝发出一束光进行联络,则宝宝观测到该光束的传播速度为( )
 如图所示,乒乒乘坐速度为0.8c(c为光速)的宇宙飞船追赶正前方的宝宝,宝宝的飞行速度为0.6c,乒乒向宝宝发出一束光进行联络,则宝宝观测到该光束的传播速度为( )
如图所示,乒乒乘坐速度为0.8c(c为光速)的宇宙飞船追赶正前方的宝宝,宝宝的飞行速度为0.6c,乒乒向宝宝发出一束光进行联络,则宝宝观测到该光束的传播速度为( )| A. | 0.4c | B. | 1.4c | C. | 1.0c | D. | 0.2c |
1.一小船在静止水中速度为5m/s,它在一条河宽为200m,水流速度为3m/s的河流中过河,则小船过河的最短时间为( )
| A. | 30s | B. | 40s | C. | 50s | D. | 60s |
8. 如图所示,有一系列斜面处在同一竖直面上,都位于竖直线OO′的右侧,倾角不同,它们的底端都是O点,有一些完全相同的滑块(可视为质点)从这些斜面上的A、B、C、D…各点同时由静止释放,下列判断正确的是( )
如图所示,有一系列斜面处在同一竖直面上,都位于竖直线OO′的右侧,倾角不同,它们的底端都是O点,有一些完全相同的滑块(可视为质点)从这些斜面上的A、B、C、D…各点同时由静止释放,下列判断正确的是( )
 如图所示,有一系列斜面处在同一竖直面上,都位于竖直线OO′的右侧,倾角不同,它们的底端都是O点,有一些完全相同的滑块(可视为质点)从这些斜面上的A、B、C、D…各点同时由静止释放,下列判断正确的是( )
如图所示,有一系列斜面处在同一竖直面上,都位于竖直线OO′的右侧,倾角不同,它们的底端都是O点,有一些完全相同的滑块(可视为质点)从这些斜面上的A、B、C、D…各点同时由静止释放,下列判断正确的是( )| A. | 若各斜面均光滑,且这些滑块到达0点的速率相同,则A、B、C、D…各点处在同一竖直线上 | |
| B. | 若各斜面均光滑,且这些滑块到达0点所用时间相等,则A、B、C、D…各点处在同一圆周上 | |
| C. | 若各斜面与这些滑块之间的动摩擦因数相同,滑到O点的过程中,各滑块损失的机械能相同,则A、B、C、D…各点处在同一竖直线上 | |
| D. | 若各斜面与这些滑块之间的动摩擦因数相同,滑到O点的过程中,各滑块损失的机械能相同,则A、B、C、D…各点处在同一圆周上 |
18. 某同学在做“研究平抛物体的运动”的实验时得到如图所示的轨迹,其中某次落点A点的位置不在平滑的曲线上,产生着一现象的可能原因是 ( )
某同学在做“研究平抛物体的运动”的实验时得到如图所示的轨迹,其中某次落点A点的位置不在平滑的曲线上,产生着一现象的可能原因是 ( )
 某同学在做“研究平抛物体的运动”的实验时得到如图所示的轨迹,其中某次落点A点的位置不在平滑的曲线上,产生着一现象的可能原因是 ( )
某同学在做“研究平抛物体的运动”的实验时得到如图所示的轨迹,其中某次落点A点的位置不在平滑的曲线上,产生着一现象的可能原因是 ( )| A. | 小球下滑时与斜槽间有摩擦 | |
| B. | 斜槽末端的切线方向不水平 | |
| C. | 某次实验时 小球开始下滑时位置偏低 | |
| D. | 某次实验时小球开始下滑时初速度不为零 |
5.一静止在水平地面上的物体在水平拉力F=6N的作用下做匀加速直线运动,在第一个2s内的平均速度为1m/s,已知物体与水平面间的动摩擦因数μ=0.2,试求物体的加速度大小和质量.(取g=10m/s2)
2.游泳运动员以恒定的速率朝垂直河岸方向游过某条河,若河宽一定,当水速突然增大时,关于运动员渡河经过的路程和所用时间,下列说法正确的是( )
| A. | 路程增加、时间不定 | B. | 路程增加、时间缩短 | ||
| C. | 路程增加、时间增加 | D. | 路程、时间均与水速无关 |
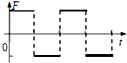
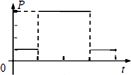
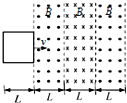 如图所示,垂直于纸面的三个有界匀强磁场的磁感应强度大小均为B,磁场宽度均为L,在磁场区域的左侧边界处,有一边长为L的正方形导体线框,总电阻为R,且线框平面与磁场方向垂直,现用外力F使线框以速度v匀速穿过磁场区域,以图示位置为计时起点,规定电流沿逆时针方向时的电动势E为正,磁感线垂直纸面向里时的磁通量Φ为正值,外力F向右为正,是以下能正确反映线框中磁能量Φ、感应电动势E、外力F和是功率P随时间变化规律的图象是( )
如图所示,垂直于纸面的三个有界匀强磁场的磁感应强度大小均为B,磁场宽度均为L,在磁场区域的左侧边界处,有一边长为L的正方形导体线框,总电阻为R,且线框平面与磁场方向垂直,现用外力F使线框以速度v匀速穿过磁场区域,以图示位置为计时起点,规定电流沿逆时针方向时的电动势E为正,磁感线垂直纸面向里时的磁通量Φ为正值,外力F向右为正,是以下能正确反映线框中磁能量Φ、感应电动势E、外力F和是功率P随时间变化规律的图象是( )