题目内容
（2010?孝感一模）假设太阳系内某行星和地球的公转轨道均为圆形，且在同一平面内，如图所示，半径较小的轨道是某行星公转的轨道，半径较大的轨道是地球公转的轨道．在地球上观测，发现该行星与太阳可呈现的视角（太阳与行星均看成质点，它们与眼睛连线的夹角）有最大值，并且最大视角的正弦值为| 16 | 25 |
分析：根据几何关系求出星球的轨道半径和地球的轨道半径的关系，结合万有引力提供向心力求出轨道半径和周期的关系，从而得出行星的公转周期．
解答：解：行星与太阳的最大视角出现的情况是地球上的人的视线看行星时，视线与行星的轨道相切，如图所示．α为最大视角，由图可知，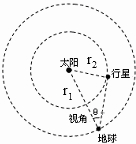
sinα=
由题意有：sinα=
所以
=
对于环绕太阳运行的任一行星有：
=mr
（式中M为太阳质量）
即
=
所以有：
=
将上面两星轨道半径比值代入有：T星=
T地=0.512年．
答：该行星的公转周期为0.512年．
sinα=
| r星 |
| r地 |
由题意有：sinα=
| 16 |
| 25 |
所以
| r星 |
| r地 |
| 16 |
| 25 |
对于环绕太阳运行的任一行星有：
| GMm |
| r2 |
| 4π2 |
| T2 |
即
| T2 |
| r3 |
| 4π2 |
| GM |
所以有：
| T星2 |
| T地2 |
| r星3 |
| r地3 |
将上面两星轨道半径比值代入有：T星=
| 64 |
| 125 |
答：该行星的公转周期为0.512年．
点评：解决本题的关键掌握万有引力提供向心力这一理论，本题对数学能力要求较高，需加强训练．
练习册系列答案
开心蛙状元测试卷系列答案
相关题目
（2010?孝感一模）如图所示，细绳的上端系在斜面的固定挡板上，下端连着物块B，轻弹簧一端与物块B相连，斜面与物块B接触处和接触处以上部分光滑（无摩擦力），斜面与物块B接触处以下部分粗糙，物块A、B的质量分别为m1、m2，物块A与斜面间的动摩擦因数为?，斜面的倾角为θ，物块A沿斜面向上滑动，刚与弹簧接触时速度大小为υ0，继续向上运动压缩弹簧并被向下弹回，物块B始终静止．弹簧的劲度系数为k，若物块A上升到最高点时细绳的拉力恰好为零．求：