题目内容
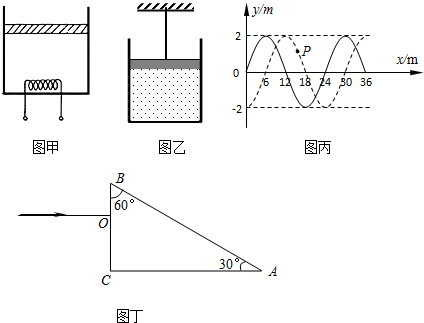
如图甲所示,在光滑绝缘的水平桌面上建立一xoy坐标系,平面处在周期性变化的电场和磁场中,电场和磁场的变化规律如图乙所示(规定沿+y方向为电场强度的正方向,竖直向下为磁感应强度的正方向).在t=0时刻,一质量为10g、电荷量为0.1C的带电金属小球自坐标原点O处,以v0=2m/s的速度沿x轴正方向射出.已知E0=0.2N/C、B0=0.2πT.求:
(1)t=1s末速度的大小和方向;
(2)1s~2s内,金属小球在磁场中做圆周运动的半径和周期;
(3)(2n-1)s~2ns(n=1,2,3,…)内金属小球运动至离x轴最远点的位置坐标.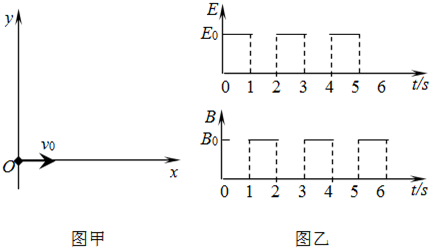
(1)t=1s末速度的大小和方向;
(2)1s~2s内,金属小球在磁场中做圆周运动的半径和周期;
(3)(2n-1)s~2ns(n=1,2,3,…)内金属小球运动至离x轴最远点的位置坐标.

分析:(1)第一秒内粒子做类似平抛运动,根据分速度公式列式求解;
(2)根据洛伦兹力提供向心力列式求解轨道半径和周期;
(3)先求出(2n-1)s的位置坐标和速度大小和方向,再求出第2ns内的轨道半径,画出轨迹,最后求离x轴最远距离.
(2)根据洛伦兹力提供向心力列式求解轨道半径和周期;
(3)先求出(2n-1)s的位置坐标和速度大小和方向,再求出第2ns内的轨道半径,画出轨迹,最后求离x轴最远距离.
解答:解:(1)在0~1s内,金属小球在电场力作用下,在x轴方向上做匀速运动vx=v0,y方向做匀加速运动vy=
t1
1s末粒子的速度v1=
=2
m/s
设v1与x轴正方向的夹角为α,则tanα=
=1,故α=450
(2)在1s~2s内,粒子在磁场中做圆周运动,由牛顿第二定律,得qv1B0=
,解得R1=
=
m
粒子做圆周运动的周期T=
=1s
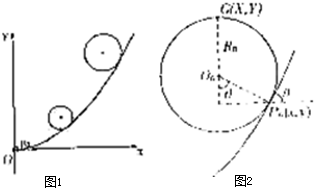
(3)粒子运动轨迹如图1所示
(2n-1)s末粒子的横坐标为x=v0t=2n(m)
纵坐标为:y=
at2=
×
×n2=n2(m)
此时粒子的速度为:vn=
=2
m/s
速度偏向角的正切值为:tanθ=
=
=n
带电粒子在(2n-1)s~2ns(n=1,2,3…)内做圆周运动的轨迹如图2所示,半径Rn=
=
m
(2n-1)s~2ns(n=1,2,3,…)内粒子运动至离x轴最远点横坐标为:X=x-Rnsinθ=(2n-
)m
纵坐标为:Y=y+Rn(1+cosθ)=(n2+
+
)m
答:(1)t=1s末速度的大小为2
m/s,方向与x轴成45°角;
(2)1s~2s内,金属小球在磁场中做圆周运动的半径为
m,周期为1s;
(3)(2n-1)s~2ns(n=1,2,3,…)内金属小球运动至离x轴最远点的位置坐标为((2n-
)m,(n2+
+
)m).
| qE0 |
| m |
1s末粒子的速度v1=
|
| 2 |
设v1与x轴正方向的夹角为α,则tanα=
| vy |
| vx |
(2)在1s~2s内,粒子在磁场中做圆周运动,由牛顿第二定律,得qv1B0=
m
| ||
| R1 |
| mv1 |
| qB0 |
| ||
| π |
粒子做圆周运动的周期T=
| 2πm |
| qB0 |
(3)粒子运动轨迹如图1所示

(2n-1)s末粒子的横坐标为x=v0t=2n(m)
纵坐标为:y=
| 1 |
| 2 |
| 1 |
| 2 |
| qE0 |
| m |
此时粒子的速度为:vn=
|
| n2+1 |
速度偏向角的正切值为:tanθ=
| vy |
| v0 |
| ||
| v0 |
带电粒子在(2n-1)s~2ns(n=1,2,3…)内做圆周运动的轨迹如图2所示,半径Rn=
| mvn |
| qB0 |
| ||
| π |
(2n-1)s~2ns(n=1,2,3,…)内粒子运动至离x轴最远点横坐标为:X=x-Rnsinθ=(2n-
| n |
| π |
纵坐标为:Y=y+Rn(1+cosθ)=(n2+
| ||
| π |
| 1 |
| π |
答:(1)t=1s末速度的大小为2
| 2 |
(2)1s~2s内,金属小球在磁场中做圆周运动的半径为
| ||
| π |
(3)(2n-1)s~2ns(n=1,2,3,…)内金属小球运动至离x轴最远点的位置坐标为((2n-
| n |
| π |
| ||
| π |
| 1 |
| π |
点评:本题中粒子奇数秒内做类似平抛运动,偶数秒内做匀速圆周运动,关键是画出运动轨迹并根据平抛运动规律和匀速圆周运动规律列式分析.

练习册系列答案
相关题目
 [选做题]本题包括A、B、C三小题,请选定其中两题,并在相应的答题区域内作答.若三题都做,则按A、B两题评分.
[选做题]本题包括A、B、C三小题,请选定其中两题,并在相应的答题区域内作答.若三题都做,则按A、B两题评分.
 如图甲所示,内壁光滑的绝热气缸竖直立于地面上,绝热活塞将一定质量的气体封闭在气缸中,活塞静止时处于A位置.现将一重物轻轻地放在活塞上,活塞最终静止在如图乙所示的B位置.设分子之间除相互碰撞以外的作用力可忽略不计,则活塞在B位置时与活塞在A位置时相比较( )
如图甲所示,内壁光滑的绝热气缸竖直立于地面上,绝热活塞将一定质量的气体封闭在气缸中,活塞静止时处于A位置.现将一重物轻轻地放在活塞上,活塞最终静止在如图乙所示的B位置.设分子之间除相互碰撞以外的作用力可忽略不计,则活塞在B位置时与活塞在A位置时相比较( )