题目内容
17. 如图所示,质量N=4kg的滑板B静止放在光滑水平面上,其右端固定一根轻质弹簧,滑板B上表面光滑,质量m=2kg的小铁块A,以水平速度v0=6m/s由滑板B左端开始沿滑板表面向右运动,g取10m/s2.求:
如图所示,质量N=4kg的滑板B静止放在光滑水平面上,其右端固定一根轻质弹簧,滑板B上表面光滑,质量m=2kg的小铁块A,以水平速度v0=6m/s由滑板B左端开始沿滑板表面向右运动,g取10m/s2.求:(1)弹簧被压缩到最短时,滑板B的速度;
(2)滑板B的最大瞬时速度.
分析 (1)弹簧被压缩到最短时,A与B的速度相同.A、B组成的系统在水平方向所受合外力为零,系统动量守恒,由动量守恒定律可以求出B的速度.
(2)当弹簧再次恢复原长时,B的速度最大.在整个过程中,系统动量守恒,机械能也守恒,由两大守恒定律可以求解.
解答 解:(1)弹簧被压缩到最短时,A与滑板B具有相同的速度,
设为v,从A开始沿滑板B表面向右运动至弹簧被压缩到最短的过程中,取向右为正方向,由A、B系统的动量守恒得:
mv0=(M+m)v,
得:v=$\frac{m{v}_{0}}{M+m}$=$\frac{2×6}{4+2}$=2 m/s.
(2)当弹簧再次恢复原长时,B的速度最大.在整个过程中,根据系统的动量守恒和机械能守恒得:
mv0=MvB+mvA,
$\frac{1}{2}m{v}_{0}^{2}$=$\frac{1}{2}M{v}_{B}^{2}$+$\frac{1}{2}m{v}_{A}^{2}$
联立解得:vB=$\frac{2m}{m+M}{v}_{0}$=$\frac{2×2}{2+4}×6$=4m/s
答:
(1)弹簧被压缩到最短时,滑板B的速度为2m/s;
(2)滑板B的最大瞬时速度是4m/s.
点评 本题关键要分析清楚物体的运动过程,知道弹簧再次恢复原长时,B的速度最大,应用动量守恒定律与能量守恒定律即可正确解题.

练习册系列答案
相关题目
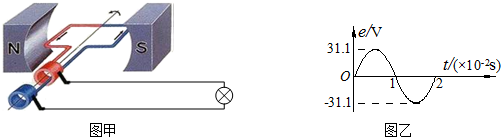
7.图甲是小型交流发电机的示意图,在匀强磁场中,一矩形金属线圈绕与磁场方向垂直的轴匀速转动,产生的电动势随时间变化的正弦规律图象如图乙所示.发电机线圈内阻为10Ω,外接一只电阻为90Ω的灯泡,不计电路的其它电阻,则( )

| A. | t=0时刻穿过线圈磁通量最大 | B. | 每秒钟内电流方向改变50次 | ||
| C. | 灯泡两端的电压为22V | D. | 0~0.01s时间内通过灯泡的电量为0 |
8.下面甲、乙两图中,一个是伏安法测电阻的实物连接图,另一个是用电流表和电压表测定电源电动势和内阻的实物连接图.

①测定电源电动势和内阻的实物连接图是图甲.按照该方法测量得到的电源电动势比真实值偏小,内阻比真实值偏小.(填“偏大”、“不变”或“偏小”).
表1
表2
②上面的表1和2是利用上面题中的实物图且当滑动变阻器的滑动触头逐渐向右移动时依次测得的实验数据表,其中与甲图对应的表格是丁表,在答题卡上画出其对应的电路图.

①测定电源电动势和内阻的实物连接图是图甲.按照该方法测量得到的电源电动势比真实值偏小,内阻比真实值偏小.(填“偏大”、“不变”或“偏小”).
表1
| V表读数/V | 0.81 | 1.21 | 1.70 | 1.81 | 2.51 |
| A表读数/A | 0.16 | 0.24 | 0.34 | 0.36 | 0.50 |
| V表读数/V | 1.37 | 1.32 | 1.24 | 1.18 | 1.05 |
| A表读数/A | 0.12 | 0.20 | 0.31 | 0.32 | 0.57 |
5.关于核反应方程类型,下列说法正确的是( )
| A. | ${\;}_{11}^{24}$Na→${\;}_{12}^{24}$Mg+${\;}_{-1}^{0}$e 是α衰变 | |
| B. | ${\;}_{92}^{235}$U+${\;}_{0}^{1}$n→${\;}_{56}^{144}$Ba+${\;}_{36}^{89}$Kr+3${\;}_{0}^{1}$n 是裂变 | |
| C. | ${\;}_{1}^{2}$H+${\;}_{1}^{3}$H→${\;}_{2}^{4}$He+${\;}_{0}^{1}$n 是裂变 | |
| D. | ${\;}_{86}^{222}$Rn→${\;}_{84}^{218}$Po+${\;}_{2}^{4}$He 是β衰变 |
12.如图甲所示,在水平向右的磁场中,竖直放置一个单匝金属圆线圈,线圈所围面积为0.1m2,线圈电阻为0.1Ω,磁场的磁感应强度大小B随时间t的变化规律如图乙所示,规定从左向右看顺时针方向为线圈中感应电流的正方向,则( )


| A. | 第2s内线圈有收缩的趋势 | B. | 第3s内线圈的发热功率最大 | ||
| C. | 第4s感应电流的方向为正方向 | D. | 0-5s内感应电流的最大值为0.1A |
2.下列有关光的说法中正确的是( )
| A. | 自贡电信的光纤通信主要是利用了光的折射现象 | |
| B. | 在光的双缝干涉实验中,若仅将入射光由绿光改为红光,则干涉条纹间距变窄 | |
| C. | 利用双缝干涉仪等器材可以测量光的波长 | |
| D. | 光的偏振现象进一步证实了光是纵波 |
6.以下不属于比值法定义式的是( )
| A. | a=$\frac{△v}{△t}$ | B. | p=$\frac{W}{t}$ | C. | E=$\frac{U}{d}$ | D. | Φ=$\frac{{E}_{t}}{q}$ |
7.在平直的路面上,机车拉着车厢匀加速前进,下列说法正确的是( )
| A. | 车厢对机车的拉力大于机车对车厢的拉力 | |
| B. | 车厢对机车的拉力小于机车对车厢的拉力 | |
| C. | 车厢对机车的拉力大于车厢受到的阻力 | |
| D. | 车厢对机车的拉力小于车厢受到的阻力 |
