题目内容
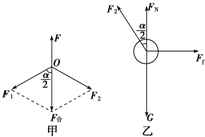
 如图所示,两个完全相同的球,重力大小均为G,两球与水平地面间的动摩擦因数都为μ,且假设最大静摩擦力等于滑动摩擦力,一根轻绳两端固结在两个球上,在绳的中点施加一个竖直向上的拉力,当绳被拉直后,两段绳间的夹角为α.问当F至少为多大时,两球将会发生滑动?
如图所示,两个完全相同的球,重力大小均为G,两球与水平地面间的动摩擦因数都为μ,且假设最大静摩擦力等于滑动摩擦力,一根轻绳两端固结在两个球上,在绳的中点施加一个竖直向上的拉力,当绳被拉直后,两段绳间的夹角为α.问当F至少为多大时,两球将会发生滑动?分析:当用力拉绳子的中点时,绳子对两球有作用力,使它们要发生滑动.则对球受力分析由力的合成,得出两段绳间的夹角为α时绳子力大小,从而再对O点进行受力分析,再由力的合成去寻找力的三角函数关系.
解答:解:对结点O受力分析如图甲所示,由平衡条件得:
F1=F2=
对任一球(如右球)受力分析如图乙所示,球发生滑动的临界条件是:F2sin
=μFN.
又F2cos
+FN=G.
联立解得:F=
.
答:当F至少为
时,两球将会发生滑动.

F1=F2=
| F | ||
2cos
|
对任一球(如右球)受力分析如图乙所示,球发生滑动的临界条件是:F2sin
| α |
| 2 |
又F2cos
| α |
| 2 |
联立解得:F=
| 2μG | ||
μ+tan
|
答:当F至少为
| 2μG | ||
μ+tan
|
点评:在进行力处理时,三个力构成的三角形有的是构成直角三角形,有的是构成等腰三角形,有的是构成等边三角形.

练习册系列答案
相关题目
 (2012?金山区一模)如图所示,两个完全相同的波源在介质中形成的波相叠加而发生的干涉的示意图,实线表示波峰,虚线表示波谷,则( )
(2012?金山区一模)如图所示,两个完全相同的波源在介质中形成的波相叠加而发生的干涉的示意图,实线表示波峰,虚线表示波谷,则( ) (2008?上海模拟)如图所示,两个完全相同的波源在介质中形成的波相叠加而发生的干涉的示意图,实线表示波峰,虚线表示波谷,则( )
(2008?上海模拟)如图所示,两个完全相同的波源在介质中形成的波相叠加而发生的干涉的示意图,实线表示波峰,虚线表示波谷,则( )