��Ŀ����
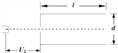
����Ŀ����ͼ����ʾ�����ݿ���Բ��������ת�������䣬����������ʩ����ħ��һ��������Ϊ ��ħ�������������ɵ�ЧΪһ�ʵ���Բ�������˶�ģ�ͣ���ͼ����ʾ������ֱƽ���ڹ̶���ǿ����Բ����뾶ΪR��A��B����ֱ�Ϊ�������ߵ�����͵㡣�ʵ��ع�������������Բ���˶�����Բ�����ǿ��������ʼ��ָ��Բ��O�Ҵ�С��ΪF�����ʵ�������![]() ͨ��A��ʱ���Թ����ѹ��Ϊ��������7��������Ħ���Ϳ����������������ٶ�Ϊg��
ͨ��A��ʱ���Թ����ѹ��Ϊ��������7��������Ħ���Ϳ����������������ٶ�Ϊg��

(1)���ʵ��������
(2)�ʵ�����������Բ���˶������У�������������С�㶨����֤���ʵ��A��B�����ѹ����Ϊ��ֵ��
(3)������������С��Ϊ2F��Ϊȷ���ʵ���������Բ���˶������ʵ�ͨ��B��������ʡ�
���𰸡�(1) ![]() (2)
(2) ![]() (3)
(3) ![]()
�����������������������������������������ߵ����������Դ��������������ʽ������⣻����ߵ����͵��ٶ������ٽ�������֧����Ϊ0��������������ʽ�ֱ������ߵ����͵������ٶ���
(1)��A��: ![]() ��
��
����ţ�ٵ�������: ![]() ��
��
�ɢ٢�ʽ������: ![]() ��
��
(2)�ʵ������Բ���˶�,��A��:����ţ�ٵڶ�����: ![]() ��
��
����ţ�ٵ�������: ![]() ��
��
��B��,����ţ�ٵڶ�����: ![]() ��
��
����ţ�ٵ�������: ![]() ��
��
��A�㵽B�����,���ݻ�е���غ㶨��: ![]() ��
��
�ɢܢݢޢߢ�������: ![]() Ϊ��ֵ���õ�֤����
Ϊ��ֵ���õ�֤����
(3)��B��,����ţ�ٵڶ�����: ![]()
��FB=0,�ʵ��ٶ����, ![]()
![]() ��
��
�ɢۢ��������: ![]()

 ������������ϵ�д�
������������ϵ�д�