题目内容
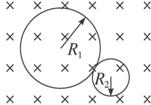
 静止在匀强磁场中的某放射性元素的原子核,当它放出一个α粒子后,其速度方向与磁场方向垂直,测得α粒子和反冲核轨道半径之比为44:1,如图所示,则( )
静止在匀强磁场中的某放射性元素的原子核,当它放出一个α粒子后,其速度方向与磁场方向垂直,测得α粒子和反冲核轨道半径之比为44:1,如图所示,则( )分析:核衰变过程动量守恒,反冲核与释放出的粒子的动量大小相等,结合带电粒子在匀强磁场中圆周运动的半径公式可得小粒子与反冲核的电荷量之比
解答:解析:微粒之间相互作用的过程中遵守动量守恒定律,由于初始总动量为零,则末动量也为零,即α粒子和反冲核的动量大小相等,方向相反.由于释放的α粒子和反冲核均在垂直于磁场的平面内,且在洛伦兹力作用下做圆周运动.
由Bqv=
得:R=
.
若原来放射性元素的核电荷数为Q,则对α粒子:R1=
.
对反冲核:R2=
.
由于p1=p2,得R1:R2=44:1,得Q=90.
反冲核的核电荷数为90-2=88.
它们的速度大小与质量成反比,故D错误.正确选项为A、B、C.
答案:ABC
由Bqv=
| mv2 |
| R |
| mv |
| Bq |
若原来放射性元素的核电荷数为Q,则对α粒子:R1=
| p1 |
| B?2e |
对反冲核:R2=
| p2 |
| B(Q-2)e |
由于p1=p2,得R1:R2=44:1,得Q=90.
反冲核的核电荷数为90-2=88.
它们的速度大小与质量成反比,故D错误.正确选项为A、B、C.
答案:ABC
点评:原子核的衰变过程类比于爆炸过程,满足动量守恒,而带电粒子在匀强磁场中圆周运动的半径公式中的分子恰好是动量的表达式,要巧妙应用

练习册系列答案
 寒假学与练系列答案
寒假学与练系列答案
相关题目