题目内容
【题目】如图所示，竖直圆筒内壁光滑，高度20m，半径为R=15cm，固定在水平面上，顶部边沿有入口A．质量为1kg的小球用长为L=0.1m的绳子系在天花板上，将小球拉起一定高度释放，绳子最大拉力为20N，小球在A点边沿恰好与绳子断开，小球沿直径AB飞入圆筒，小球在筒内碰撞前后水平方向的速度等大反向，竖直方向的速度不变，碰撞时间忽略不计，取g=10m/s2，求：
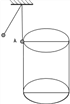
（1）小球在筒内碰撞的次数
（2）最后落地点位置距离A点的水平距离．
【答案】（1）66 ;（2）0.2m
【解析】（1）小球在最低点，根据牛顿第二定律得： 
，其中：T=20N，
解得：v0=10m/s
小球竖直方向做自由落体运动，则运动的时间为： 
此时间内小球水平方向运动的总路程为：s=v0t=20m，
每碰撞一次，小球运动的水平路程为：s′=2R=2×0.15m=0.3m，
则碰撞的次数为： 
，
则小球在筒内碰撞的次数为66次；
（2）碰撞66次时，小球到达左侧，右向右运动
s′＝0.2m落地，所以最后落地点位置距离A点的水平距离为0.2m．
练习册系列答案
期末1卷素质教育评估卷系列答案
相关题目
