题目内容
如图所示,一半径R=0.2m的水平圆盘绕过圆心的竖直轴转动,圆盘边缘有一质量m =1.0kg的小滑块。当圆盘转动的角速度逐渐增大到某一数值时,滑块刚好从圆盘边缘处滑落,进入轨道ABC。已知AB段为光滑的圆弧形轨道,轨道半径r =2.5m,B点是圆弧形轨道与水平地面的相切点,A点与B点的高度差h ="1.2m" ;倾斜轨道BC与圆轨道AB对接且倾角为37°,滑块与圆盘及BC轨道间的动摩擦因数均为μ =0.5,滑块在运动过程中始终未脱离轨道,不计滑块在A点和B点处的机械能损失,设最大静摩擦力等于滑动摩擦力,取g=10m/s2,sin37°=0.6,cos37°=0.8。
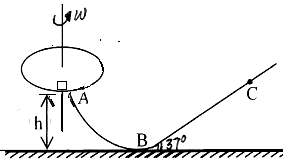
(1)求滑块刚好从圆盘上滑落时,圆盘的角速度;
(2)求滑块到达弧形轨道的B点时对轨道的压力大小;
(3)滑块从到达B点时起,经0.6s正好通过C点,求BC之间的距离。

(1)求滑块刚好从圆盘上滑落时,圆盘的角速度;
(2)求滑块到达弧形轨道的B点时对轨道的压力大小;
(3)滑块从到达B点时起,经0.6s正好通过C点,求BC之间的距离。
(1)5rad/s(2)20N(3)1.24m
试题分析:(1)滑块在圆盘上做圆周运动时,静摩擦力充当向心力,由牛顿第二定律,可得:μmg=mω2R (1分 )
代入数据解得:ω=
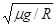 =5rad/s (1分)
=5rad/s (1分)(2)滑块在A点时的速度:vA=ωR=1m/s (1分)
滑块在从A到B的运动过程中机械能守恒: mgh+ mvA2/2= mvB2/2 (1分)
解得: vB=5m/s (1分)
在B点,由牛顿第二定律,可得:
 (1分)
(1分) 解得:
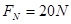 滑块对轨道的压力大小为20N。 (1分 )
滑块对轨道的压力大小为20N。 (1分 )(3)滑块沿BC段向上运动时的加速度大小:a1=g(sin37°+μcos37°)=10m/s2 (1分)
滑块沿BC段向上运动的时间:t1= vB/ a1="0.5s" <0.6s 故滑块会返回一段时间 (1分)
向上运动的位移: S1=vB2/2a1=1.25m (1分)
返回时的加速度大小:a2=g(sin37°-μcos37°)=2m/s2 (1分)
S2="1/2" a2(t-t1)2=0.01m (1分)
BC间的距离:sBC= S1- S2 =1.24m (1分)
点评:本题关键把物体的各个运动过程的受力情况和运动情况分析清楚,然后运用牛顿第二定律和运动学公式求解.

练习册系列答案
相关题目


 ?
?